दिए गए नंबरों को कैसे पेश करें और। कंप्यूटर में संख्याओं का प्रतिनिधित्व

आमतौर पर, मशीन में प्रवेश करते समय ऋणात्मक दशमलव संख्या स्वचालित रूप से रिवर्स या अतिरिक्त बाइनरी कोड में परिवर्तित हो जाती है और इस रूप में संचालन में स्थानांतरित, स्थानांतरित और शामिल होती है। कार से ऐसी संख्याएं प्राप्त करते समय, ऋणात्मक दशमलव संख्याओं में रूपांतरण को उलट दें।अधिकांश कंप्यूटरों में, घटाव ऑपरेशन का उपयोग नहीं किया जाता है। इसके बजाय, उलटा या अतिरिक्त कोड जोड़ने और घटाया गया है। यह आपको एएलयू के डिजाइन को काफी सरल बनाने की अनुमति देता है।

4.2। पूर्णांक पर अंकगणितीय संचालन

आइए हम पूर्णांक पर अंकगणितीय परिचालन करने के प्रश्न पर संक्षेप में विचार करें। संख्या ए और बी जोड़ते समय, चार मुख्य मामले हैं:

1. ए और बी सकारात्मक हैं। संक्षेप में, संकेत के अंक सहित सभी अंक जोड़े गए हैं। चूंकि सकारात्मक शर्तों के संकेत अंक शून्य हैं, इसलिए योग चिह्न का अंक भी शून्य है। उदाहरण के लिए: 0 0000011 (ए = 3) + 0 0000111 (बी = 7) = 0 0001010 (10) 10

सही परिणाम प्राप्त हुआ

2.    ए सकारात्मक है, बी नकारात्मक है और ए से अधिक परिमाण में पूर्ण है उदाहरण के लिए: 3 + (- 10) = - 7  0 0000011 (सीधा कोड) + 1 1110101 (व्यस्त संख्या कोड

10) = 1 1111000 (संख्या -7 का उलटा कोड) सही परिणाम उलटा कोड में प्राप्त किया गया था। प्रत्यक्ष कोड में अनुवाद करते समय, परिणाम के डिजिटल भाग के बिट्स उलटा हो जाते हैं: 1 0000111 = -7 10।

3.   ए सकारात्मक है, बी नकारात्मक है और ए से कम परिमाण में पूर्ण है उदाहरण के लिए: 10 + (- 3) = 7  0 0001010 (सीधा कोड) + 1 1111100 (उलटा संख्या कोड

3) = 1 0000110 कंप्यूटर प्रारंभ में प्राप्त गलत परिणाम (7 के बजाय 6) को सुधारता है। यूनिट को साइन बिट से राशि के निचले अंक में स्थानांतरित करना और सही परिणाम 7 देता है।

4.   ए और बी नकारात्मक हैं। उदाहरण के लिए: (-3) + (- 7) = - 10  1 1111100 (रिटर्न कोड -3 है) + 1 1111000 (संख्या -7 का रिटर्न कोड) = 1 1110100. परिणाम प्रारंभ में गलत है (रिवर्स के बजाय संख्या -11 10 का रिटर्न कोड कोड संख्या -10 10 है) कंप्यूटर यूनिट को साइन बिट से कम ऑर्डर राशि में स्थानांतरित करके सुधारता है। परिणाम को प्रत्यक्ष कोड में अनुवाद करते समय, संख्या के डिजिटल भाग के बिट्स उलटा हो जाते हैं: 1 0001010 = -10 10।

पूर्णांक जोड़ना व्यवस्थित किया जा सकता है अतिरिक्त कोड। ऊपर चर्चा के मामले भी यहां दिए गए हैं:

1.   ए और बी सकारात्मक हैं। रिवर्स कोड के लिए विचार किए गए केस 1 से कोई अंतर नहीं है।

2.   ए सकारात्मक है, बी नकारात्मक है और ए से अधिक परिमाण में पूर्ण है उदाहरण के लिए: 3 + (- 10) = - 7  0 0000011 (सीधा कोड) + 1 1110110 (संख्या -10 का अतिरिक्त कोड) = 1 1111001 (संख्या का अतिरिक्त कोड - 7) सही परिणाम अतिरिक्त कोड में प्राप्त किया जाता है। प्रत्यक्ष कोड में अनुवाद करते समय, परिणाम के डिजिटल भाग की बिट्स उलटा हो जाती है और एक इकाई को निम्न क्रम में जोड़ा जाता है: 1 0000110 + 1 = 1 0000111 = -7 10।

3.   ए सकारात्मक है, बी नकारात्मक है और ए से कम परिमाण में पूर्ण है उदाहरण के लिए: 10 + (- 3) = 7  0 0001010 (सीधा कोड) + 1 1111101 (संख्या -3 का अतिरिक्त कोड) = 0 0000111. सही परिणाम प्राप्त किया गया था। साइन बिट कंप्यूटर डिस्कने से स्थानांतरण इकाई।

4.   ए और बी नकारात्मक हैं। उदाहरण के लिए :: (-3) + (- 7) = - 10  1 1111101 (अतिरिक्त कोड -3) + 1 1111001 (संख्या -7 का अतिरिक्त कोड) = 1 1110110 सही परिणाम अतिरिक्त कोड में प्राप्त किया गया था। स्थानांतरण इकाई   साइन कंप्यूटर निर्वहन से फेंकता है.

हस्ताक्षर किए गए पूर्णांक कोडिंग के माना जाने वाले रूपों की तुलना से पता चलता है:

कंप्यूटर एक नकारात्मक संख्या को एक अतिरिक्त कोड में कनवर्ट करने के बजाय कोड को रिवर्स करने में कम समय बिताता है, क्योंकि बाद में दो चरणों होते हैं - एक व्यस्त कोड का गठन और इसकी सबसे छोटी श्रेणी में से एक को जोड़ना;

संख्याओं के अतिरिक्त कोड के लिए अतिरिक्त निष्पादन समय उनके रिवर्स कोड से कम है ,    क्योंकि इस अतिरिक्त में साइन बिट से इकाई के परिणाम के निचले अंक तक कोई हस्तांतरण नहीं होता है।

जोड़ते समय, एक स्थिति उत्पन्न हो सकती है जब ऑपरेशन के परिणाम के ऊपरी बिट इसके लिए आवंटित स्मृति क्षेत्र में फिट नहीं होते हैं। इस स्थिति को बुलाया जाता है संख्या प्रारूप के अंक ग्रिड का ओवरफ़्लो।   ओवरफ्लो का पता लगाने और कंप्यूटर में किसी त्रुटि के बारे में सूचित करने के लिए विशेष उपकरण का उपयोग किया जाता है।

कई कंप्यूटरों में गुणन   जोड़ों और बदलावों के अनुक्रम के रूप में उत्पादित। इसके लिए, एएलयू है रजिस्टर, जिसे जमा करने वाला योजक कहा जाता है, जो ऑपरेशन की शुरुआत से पहले संख्या शून्य होता है। एक ऑपरेशन करने की प्रक्रिया में, इसे वैकल्पिक रूप से रखा जाता है। गुण्य जिस को किसी संख्या से गुणा किया जाय   और मध्यवर्ती अतिरिक्त परिणाम, और ऑपरेशन के पूरा होने पर - अंतिम परिणाम.

इस ऑपरेशन को करने में शामिल एक अन्य एएलयू रजिस्टर में पहले गुणक होता है। फिर, जैसे ही आप जोड़ते हैं, तब तक यह संख्या शून्य तक पहुंचने तक घट जाती है।

कंप्यूटर के लिए डिवीजन एक कठिन ऑपरेशन है। आमतौर पर यह लाभांश को अतिरिक्त विभाजक कोड में जोड़कर लागू किया जाता है।

4.3। कंप्यूटर में वास्तविक संख्या का प्रतिनिधित्व

गणितीय गणना में वास्तविक संख्याओं की प्रणाली निरंतर और अनंत माना जाता है, यानी। संख्याओं की सीमा और सटीकता तक ही सीमित नहीं है। हालांकि, कंप्यूटरों में, संख्याओं को सीमित संख्या में अंकों और रजिस्टरों में संग्रहीत किया जाता है। नतीजतन, मशीन में प्रतिनिधित्व करने योग्य वास्तविक संख्याओं की प्रणाली अलग (असंतुलित) और परिमित है। कार्यक्रमों में वास्तविक संख्या लिखते समय, सामान्य अल्पविराम की बजाय, यह अवधि निर्धारित करने के लिए प्रथागत है।

पीसी में, संख्याओं को दो रूपों में से एक में प्रस्तुत किया जा सकता है:

1) एक निश्चित बिंदु के साथ - एक प्राकृतिक रूप में (0.00345 एक सही अंश है, 1.23456 एक अनुचित अंश है)

2) एक फ्लोटिंग पॉइंट (कॉमा) के साथ (555.55 = 55555 10 -2 = 0.55555 10 3)

वास्तविक संख्याओं को प्रदर्शित करने के लिए, जो या तो बहुत छोटा या बहुत बड़ा हो सकता है, संख्या प्रणाली के आधार के साथ रिकॉर्डिंग संख्याओं के रूप का उपयोग करें। किसी भी संख्या ए को घातीय रूप में प्रदर्शित किया जा सकता है:

जहां एम संख्या का मंथिसा है, क्यू संख्या प्रणाली का आधार है।, एन संख्या का क्रम है।

कंप्यूटर विज्ञान की मूल बातें माना जाता है और आधुनिक पीसी हार्डवेयर का वर्णन किया गया है। सूचना विज्ञान के क्षेत्र में बुनियादी अवधारणाओं की परिभाषा के दृष्टिकोण तैयार किए गए हैं और उनकी सामग्री का खुलासा किया गया है। आधुनिक पीसी हार्डवेयर का वर्गीकरण दिया जाता है और उनकी मुख्य विशेषताएं दी जाती हैं। सभी मुख्य प्रावधान उदाहरणों द्वारा चित्रित किए गए हैं जिनमें उचित सॉफ़्टवेयर का उपयोग विशिष्ट समस्याओं को हल करने के लिए किया जाता है।

पुस्तक:

इस पृष्ठ पर अनुभाग:

बाइनरी संख्या प्रणाली में कंप्यूटर में संख्यात्मक डेटा संसाधित किया जाता है। संख्याओं को कंप्यूटर की स्मृति में बाइनरी कोड में संग्रहीत किया जाता है, जो कि शून्य और एक के अनुक्रम के रूप में होता है, और प्रारूप में एक निश्चित या फ़्लोटिंग बिंदु के साथ प्रदर्शित किया जा सकता है।

इंटेगर निश्चित-बिंदु प्रारूप में संग्रहीत हैं। भंडारण के लिए इस नंबर प्रारूप के साथ पूरी गैर-ऋणात्मक संख्याएंआवंटित स्मृति रजिस्टर, जिसमें आठ मेमोरी सेल (8 बिट्स) शामिल हैं। मेमोरी सेल का प्रत्येक अंक हमेशा संख्या के उसी अंक से मेल खाता है, और अल्पविराम निम्न और निम्न ग्रिड के बाहर कॉमा दाईं ओर स्थित होता है। उदाहरण के लिए, स्मृति 11001101 2 को स्मृति रजिस्टर में निम्नानुसार संग्रहीत किया जाएगा:

एक गैर-अभिन्न पूर्णांक का अधिकतम मान जिसे किसी निश्चित बिंदु प्रारूप में किसी रजिस्टर में संग्रहीत किया जा सकता है, सूत्र से निर्धारित किया जा सकता है: 2 एन -1 कहां एन -संख्या के अंकों की संख्या। अधिकतम संख्या 2 8 - 1 = 255 10 = 11111111 2 और न्यूनतम 0 10 = 00000000 2 के बराबर होगी। इस प्रकार, गैर-ऋणात्मक पूर्णांक के परिवर्तन की सीमा 0 से 255 10 तक होगी।

द्विआधारी संख्या प्रणाली में दशमलव प्रणाली के विपरीत, जब एक बाइनरी संख्या कंप्यूटरीकृत होती है, तो संख्या के संकेत को इंगित करने वाले कोई प्रतीक नहीं होते हैं: सकारात्मक (+) या नकारात्मक (-); इसलिए, प्रतिनिधित्व करने के लिए हस्ताक्षरित पूर्णांकबाइनरी सिस्टम संख्या का प्रतिनिधित्व करने के लिए दो प्रारूपों का उपयोग करता है: हस्ताक्षरित मूल्य का प्रारूप और अतिरिक्त कोड का प्रारूप। पहले मामले में, हस्ताक्षर किए गए पूर्णांक को संग्रहीत करने के लिए दो मेमोरी रजिस्ट्रार (16 बिट्स) आवंटित किए जाते हैं, जिसमें संख्या के संकेत के तहत अग्रणी अंक (बाएं) का उपयोग किया जा रहा है: यदि संख्या सकारात्मक है, तो 0 को नकारात्मक बिट में लिखा गया है, यदि ऋणात्मक है, तो 1. उदाहरण के लिए , संख्या 536 10 = 0000001000011000 2 को स्मृति रजिस्टरों में निम्नानुसार दर्शाया जाएगा:

और ऋणात्मक संख्या -536 10 = 1000001000011000 2 रूप में है:

एक संकेत के साथ किसी संख्या के मूल्य के प्रारूप में अधिकतम सकारात्मक संख्या या न्यूनतम नकारात्मक (खाते के तहत एक अंक के प्रतिनिधित्व को ध्यान में रखते हुए) बराबर है 2 एन -1   - 1 = 2 16-1 - 1 = 2 15 - 1 = 32767 10 = 111111111111111 2 और संख्याओं की सीमा -32767 10 से 32767 तक की सीमा में होगी।

अक्सर, बाइनरी सिस्टम प्रारूप में हस्ताक्षर किए गए पूर्णांक का प्रतिनिधित्व करने के लिए एक बाइनरी कोड प्रारूप का उपयोग किया जाता है, जो एक कंप्यूटर में एक अंकगणित घटाव ऑपरेशन को एक अतिरिक्त ऑपरेशन के साथ बदलने की अनुमति देता है, जो माइक्रोप्रोसेसर की संरचना को बहुत सरल बनाता है और इसकी गति को बढ़ाता है।

इस प्रारूप में नकारात्मक पूर्णांक का प्रतिनिधित्व करने के लिए, एक अतिरिक्त कोड का उपयोग किया जाता है, जो नकारात्मक संख्या को शून्य से जोड़ता है। एक अतिरिक्त कोड में एक संपूर्ण नकारात्मक संख्या का अनुवाद निम्नलिखित परिचालनों का उपयोग करके किया जाता है:

1) प्रत्यक्ष कोड की संख्या के मॉड्यूल लिखें एन (एन =16) बाइनरी अंक;

2) संख्या के व्यस्त कोड प्राप्त करें (संख्या के सभी अंकों को उलटा करें, यानी शून्य के साथ सभी इकाइयों को प्रतिस्थापित करें, और इकाइयों के साथ शून्य);

3) इकाई को निचले क्रम में प्राप्त रिवर्स कोड में जोड़ें।

उदाहरण के लिए, इस प्रारूप में संख्या -536 10 के लिए मॉड्यूल 0000001000011000 2 होगा, रिटर्न कोड 111111011111100111 होगा, और अतिरिक्त कोड 111111011110101000 होगा। हम कैलकुलेटर का उपयोग करके अतिरिक्त कोड के प्राप्त मूल्य की जांच करेंगे। ऐसा करने के लिए, संख्या -536 10 के मॉड्यूलस का मान दर्ज करें, यानी, संख्या 536 10, और वैकल्पिक बटन का उपयोग करना बिन   इस संख्या को, दशमलव संख्या प्रणाली में दर्शाया गया है, बाइनरी सिस्टम में, पहले वैकल्पिक बटन स्थापित किया गया है 2 बाइट्स   बटन दबाकर नहीं   कैलकुलेटर, हम एक संख्या के व्यस्त कोड प्राप्त करते हैं, और एक बाइनरी एक रिटर्न कोड में जोड़ते हैं - एक अतिरिक्त कोड। अंतिम परिणाम प्रोग्राम की कैलक्यूलेटर विंडो (चित्र 2.6) में प्राप्त किया जाएगा। आप भी सरल कर सकते हैं: कैलक्यूलेटर पर संख्या -536 10 डायल करके और बटन को सक्रिय करके बिन, बाइनरी संख्या प्रणाली में इस संख्या का अतिरिक्त कोड प्राप्त करें।

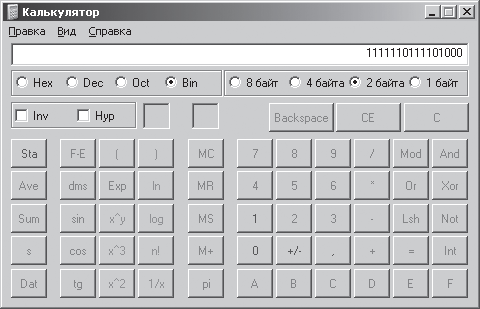
अंजीर। 2.6। अतिरिक्त कोड प्राप्त करने का नतीजा

यह याद रखना चाहिए कि एक सकारात्मक संख्या का अतिरिक्त कोड संख्या ही है।

16-बिट कंप्यूटर प्रतिनिधित्व के अलावा हस्ताक्षरित पूर्णांक संग्रहीत करने के लिए, जब दो मेमोरी रजिस्टरों का उपयोग किया जाता है (इस संख्या प्रारूप को हस्ताक्षरित लघु पूर्णांक प्रारूप भी कहा जाता है), माध्य और लंबे हस्ताक्षरित पूर्णांक प्रारूपों का उपयोग किया जाता है। चार रजिस्ट्रार (4 x 8 = 32 बिट्स) का उपयोग औसत प्रारूप में संख्याओं का प्रतिनिधित्व करने के लिए किया जाता है, और आठ रजिस्टरों (8 x 8 = 64 बिट्स) का उपयोग लंबे संख्या प्रारूप में संख्याओं का प्रतिनिधित्व करने के लिए किया जाता है। मध्यम और लंबी संख्या के प्रारूप के लिए मानों की श्रेणियां क्रमशः बराबर होंगी: - (2 31 - 1) ... + 2 31 - 1 और - (2 63 -1) ... + 2 63 - 1।

फिक्स्ड-पॉइंट प्रारूप में संख्याओं के कंप्यूटर प्रतिनिधित्व के फायदे और नुकसान होते हैं। फायदे में अंकगणितीय परिचालन के कार्यान्वयन के लिए संख्याओं और एल्गोरिदम के प्रतिनिधित्व की सादगी शामिल है, नुकसान संख्याओं के प्रतिनिधित्व की सीमित सीमा है, जो कई व्यावहारिक समस्याओं (गणितीय, आर्थिक, भौतिक, आदि) को हल करने के लिए पर्याप्त नहीं हो सकता है।

वास्तविक संख्या (परिमित और अनंत दशमलव अंश) को कंप्यूटर पर फ़्लोटिंग पॉइंट प्रारूप में संसाधित और संग्रहीत किया जाता है। इस प्रारूप के साथ, रिकॉर्ड में अल्पविराम की स्थिति भिन्न हो सकती है। कोई असली संख्या आरफ़्लोटिंग-पॉइंट प्रारूप का प्रतिनिधित्व इस प्रकार किया जा सकता है:

जहाँ ए -मंथिसा संख्या; एच -आधार संख्या प्रणाली; पी -संख्या का क्रम

दशमलव संख्या प्रणाली के लिए अभिव्यक्ति (2.7) फॉर्म लेता है:

बाइनरी के लिए -

ऑक्टल के लिए -

हेक्साडेसिमल के लिए -

किसी संख्या के प्रतिनिधित्व के इस रूप को सामान्य भी कहा जाता है। आदेश में बदलाव के साथ, संख्या में अल्पविराम को स्थानांतरित किया जाता है, यानी, क्योंकि यह बाएं या दाएं तरफ तैरता है। इसलिए, संख्याओं का प्रतिनिधित्व करने का सामान्य रूप फ़्लोटिंग पॉइंट फॉर्म कहा जाता है। 15.5 की दशमलव संख्या, उदाहरण के लिए, फ़्लोटिंग-पॉइंट प्रारूप में: 0.155 · 10 2 के रूप में प्रदर्शित किया जा सकता है; 1.55 · 10 1; 15.5 · 10 0; 155.0 · 10 -1; 1550.0 · 10 -2, आदि। 15.5 फ्लोटिंग पॉइंट का यह दशमलव नोटेशन कंप्यूटर प्रोग्राम लिखते समय और कंप्यूटर में प्रवेश करते समय उपयोग नहीं किया जाता है (कंप्यूटर इनपुट डिवाइस केवल रैखिक डेटा रिकॉर्डिंग को समझते हैं)। इस पर आधारित, अभिव्यक्ति (2.7) दशमलव संख्याओं का प्रतिनिधित्व करने और उन्हें कंप्यूटर में दर्ज करने के लिए रूप में परिवर्तित किया जाता है

जहाँ आर -संख्या का क्रम

यानी, संख्या प्रणाली 10 के आधार के बजाय, वे पत्र लिखते हैं ई,एक अल्पविराम के बजाय - एक बिंदु, और गुणा संकेत नहीं रखा जाता है। इस प्रकार, एक फ्लोटिंग पॉइंट और एक रैखिक रिकॉर्ड (कंप्यूटर प्रतिनिधित्व) के साथ प्रारूप में संख्या 15.5 फॉर्म में लिखा जाएगा: 0.155Е2; 1.55E1; 15.5E0; 155.0E-1; 1550.0 ई -2, आदि

संख्या प्रणाली के बावजूद, किसी भी फ़्लोटिंग पॉइंट फॉर्म को संख्याओं के अनंत सेट द्वारा दर्शाया जा सकता है। रिकॉर्डिंग के इस रूप को गैर-सामान्यीकृत कहा जाता है। फ्लोटिंग-पॉइंट नंबरों का विशिष्ट रूप से प्रतिनिधित्व करने के लिए, संख्या को लिखने के सामान्यीकृत रूप का उपयोग करें, जिसमें संख्या के मंटिसा को स्थिति को पूरा करना होगा

जहाँ | ए | -   मंथिसा संख्या का पूर्ण मूल्य।

स्थिति (2.9) का मतलब है कि मंटिसा एक नियमित अंश होना चाहिए और दशमलव बिंदु के बाद एक गैर-शून्य संख्या होनी चाहिए, या, दूसरे शब्दों में, यदि मंटिसा में दशमलव बिंदु nonzero है, तो संख्या को सामान्यीकृत कहा जाता है। इस प्रकार, एक फ्लोटिंग प्वाइंट के रूप में सामान्यीकृत रूप (सामान्यीकृत मंटिसा) में संख्या 15.5 इस तरह दिखेगी: 0.155 · 10 2, यानी सामान्यीकृत मंथिसा होगा एक   = 0.155 और ऑर्डर पी   = 2, या 0.155E2 संख्या के कंप्यूटर प्रतिनिधित्व में।

एक फ़्लोटिंग कॉमा के रूप में संख्याओं में एक निश्चित प्रारूप होता है और कंप्यूटर की स्मृति में चार (32 बिट्स) या आठ बाइट्स (64 बिट्स) पर कब्जा होता है। यदि कंप्यूटर की स्मृति में संख्या 32 अंकों पर है, तो यह सामान्य सटीक संख्या है, यदि यह 64 अंकों है, तो यह एक डबल परिशुद्धता संख्या है। फ़्लोटिंग पॉइंट नंबर लिखते समय, मंटिसा साइन, ऑर्डर साइन, मंथिसा साइन एंड ऑर्डर स्टोर करने के लिए बिट्स आवंटित किए जाते हैं। संख्याओं के क्रम में आवंटित अंकों की संख्या, संख्याओं की विविधता की सीमा निर्धारित करती है, और मंटिसा को स्टोर करने के लिए अलग किए गए अंकों की संख्या निर्धारित करती है, जिसकी संख्या निर्धारित होती है।

फ़्लोटिंग-पॉइंट प्रारूप में प्रदर्शित संख्याओं पर अंकगणितीय परिचालन (जोड़ और घटाव) करने पर, निम्नलिखित प्रक्रिया (एल्गोरिदम) लागू की जाती है:

1) संख्याओं के आदेश जिन पर अंकगणितीय परिचालन किए जाते हैं, गठबंधन होते हैं (पूर्ण संख्या में छोटे संख्या का क्रम बड़ी संख्या के क्रम के मूल्य में बढ़ जाता है, मंथिसा एक ही समय में घटता है);

2) अंकों के मंथिसा पर अंकगणितीय परिचालन किए जाते हैं;

3) प्राप्त परिणाम सामान्यीकृत है।

आइए उपरोक्त उदाहरणों के साथ समझाएं।

हम फ्लोटिंग-पॉइंट प्रारूप में दो संख्याओं को 0.5 · 10 2 और 0.8 · 10 3 जोड़ते हैं।

निर्णय

आइए हम आदेशों के संरेखण और मंथिस 0.05 · 10 3 + 0.8 · 10 3 = 0.85 · 10 3 के अतिरिक्त कार्य करते हैं। प्राप्त मंटिसा 0.85 सामान्यीकृत है, क्योंकि यह स्थिति (2.9) को संतुष्ट करता है।

चलो एक फ्लोटिंग कॉमा के प्रारूप में दो संख्याओं 0,1 · 2 2 और 0,1 · 2 3 के अतिरिक्त बनाते हैं।

निर्णय

आइए ऑर्डर के संरेखण और मंटिस के अतिरिक्त: 0.01 · 2 3 + 0.1 · 2 3 = 0.11 · 2 3 करें। परिणामी 0.11 मंथिसा सामान्यीकृत है, क्योंकि यह स्थिति (2.9) को संतुष्ट करता है।

गणितीय गणनाओं में वास्तविक संख्याओं के संख्याओं के प्रतिनिधित्व की सीमा और सटीकता पर कोई प्रतिबंध नहीं है। हालांकि, कंप्यूटरों में, संख्याओं को सीमित संख्या में अंकों और रजिस्टरों में संग्रहीत किया जाता है। इसलिये शुद्धता   की प्रस्तुति   असली संख्याकार में प्रतिनिधित्व योग्य, सीमित है और सीमा सीमित है।

कार्यक्रमों में वास्तविक संख्या लिखते समय, सामान्य अल्पविराम की बजाय, यह अवधि निर्धारित करने के लिए प्रथागत है। किसी भी वास्तविक संख्या को संख्या प्रणाली के आधार के साथ लेखन संख्या के रूप में दर्शाया जा सकता है।

उदाहरण 4.4।   संख्या प्रणाली के आधार के साथ रिकॉर्डिंग संख्याओं के रूप में दशमलव संख्या 1.756 निम्नानुसार प्रदर्शित की जा सकती है:

1.756 . 10 0 = 0.1756 . 10 1 = 0.01756 . 10 2 = ...

17.56 . 10 -1 = 175.6 . 10 -2 = 1756.0 . 10 -3 = ... .

फ़्लोटिंग प्वाइंट प्रतिनिधित्व संख्या का प्रतिनिधित्व कहा जाता है एन   आधार के साथ संख्या प्रणाली में क्ष   के रूप में :

एन = एम *। क्यू पी ,

जहाँ मीटर - एक गुणक संख्या (मंटिसा) के सभी अंक युक्त, पी   ऑर्डर नामक एक पूर्णांक है।

यदि "महत्वपूर्ण" बिंदु पहले महत्वपूर्ण अंक से पहले मंटिसा में स्थित है, तो मंटिसा के लिए आरक्षित अंकों की एक निश्चित संख्या के साथ, संख्या में महत्वपूर्ण अंकों की अधिकतम संख्या रिकॉर्ड की जा सकती है, यानी, कार में संख्या का प्रतिनिधित्व करने में अधिकतम सटीकता।

यदि मंटिसा में बिंदु (कॉमा) के बाद पहला अंक शून्य नहीं है, तो यह संख्या कहा जाता है सामान्यीकृत .

मंथिसा और आदेश क्ष - सामान्य संख्या आमतौर पर आधार के साथ सिस्टम में दर्ज की जाती है क्ष , और आधार स्वयं दशमलव प्रणाली में है।

उदाहरण 4.5।   आइए दशमलव प्रणाली में किसी संख्या के सामान्यीकृत प्रतिनिधित्व के उदाहरण दें:

2178.01 =0.217801 * 10 4

0.0045 =0.45 * 10 -2

बाइनरी उदाहरण:

10110.01 = 0.1011001 * 2 101 (आदेश 101 2 = 5 10)

आधुनिक कंप्यूटर फ़्लोटिंग-पॉइंट वास्तविक संख्याओं के लिए कई अंतर्राष्ट्रीय मानक स्टोरेज स्वरूपों का समर्थन करते हैं जो सटीकता में भिन्न होते हैं, लेकिन उनमें सभी की एक ही संरचना होती है। वास्तविक संख्या तीन भागों में संग्रहित की जाती है: मंटिसा का संकेत, स्थानांतरित आदेश और मंटिसा:

ऑफसेट ऑर्डर n-बिटी सामान्यीकृत संख्या की गणना निम्नानुसार की जाती है: यदि आदेश के कार्य के लिए इसे हाइलाइट किया गया है कश्मीर   बिट्स, फिर अतिरिक्त कोड में प्रस्तुत ऑर्डर का सही मान, एक ऑफसेट बराबर (2 के -1 -1) जोड़ें।

इस प्रकार, एक आदेश जो कि -128 से +127 तक की सीमा में मान लेता है, को 0 से 255 तक की श्रेणी में ऑफसेट ऑर्डर में परिवर्तित कर दिया जाता है। ऑफसेट ऑर्डर को एक हस्ताक्षरित नंबर के रूप में संग्रहीत किया जाता है, जो ऑर्डर की तुलना, जोड़ और घटाव को सरल बनाता है, और तुलना को सरल बनाता है सामान्यीकृत संख्या खुद।

आदेश के लिए आवंटित अंकों की संख्या सबसे छोटी गैर-शून्य संख्या से सबसे बड़ी संख्या तक की सीमा को प्रभावित करती है जिसे किसी दिए गए प्रारूप के लिए कार में प्रदर्शित किया जा सकता है। जाहिर है, मंटिसा को सौंपा गया अधिक अंक, संख्या प्रतिनिधित्व की सटीकता जितनी अधिक होगी। इस तथ्य के कारण कि सामान्यीकृत वास्तविक संख्या में मंथिसा का उच्च हिस्सा हमेशा 1 होता है, यह उच्च बिट स्मृति में संग्रहीत नहीं होता है।

सबसे अधिक युक्त कोई बाइनरी पूर्णांक मीटर   निर्वहन बिना विकृति के वास्तविक प्रारूप में परिवर्तित किया जा सकता है।

तालिका 4.3। वास्तविक संख्याओं के प्रतिनिधित्व के लिए मानक प्रारूप

उदाहरण 4.6।एक प्रारूप में सामान्यीकृत संख्याओं का प्रतिनिधित्व।

हम बताते हैं कि संख्या 37.16 10 कैसे संग्रहीत की जाएगी। बाइनरी संख्या में कनवर्ट करते समय, सटीक अनुवाद 100101, (00101000111101011100) विफल रहता है - ब्रैकेट में संलग्न आंशिक भाग अवधि में दोहराया जाता है।

हम संख्या को सामान्यीकृत रूप में अनुवाद करते हैं: 0.100101 (0010100011110101010000) * 2,110

32-बिट प्रारूप में वास्तविक संख्या की कल्पना करें:

1. संख्या "+" का संकेत, इसलिए, साइन बिट (31) में हम 0 दर्ज करते हैं;

2. ऑर्डर सेट करने के लिए, अतिरिक्त बिट्स में प्रदर्शित ऑर्डर के वास्तविक मूल्य पर 8 बिट्स आवंटित किए जाते हैं, हम ऑफसेट (2 7 -1) = 127 जोड़ते हैं। चूंकि ऑर्डर सकारात्मक है, डायरेक्ट ऑर्डर कोड अतिरिक्त के साथ मेल खाता है, हम स्थानांतरित ऑर्डर की गणना करते हैं: 00000110 + 01111111 = 10000101

हम परिणामी शिफ्ट ऑर्डर दर्ज करते हैं।

3. हम मंटिसा के उच्च क्रम को हटाते हुए मंटिसा लाते हैं (यह हमेशा 1 के बराबर होता है);

इस उदाहरण में, हम केवल 24 अंकों को स्थानांतरित करने में सक्षम थे, शेष संख्या के प्रतिनिधित्व में सटीकता के नुकसान के साथ बाकी खो गए थे।

इंटीजर सबसे सरल संख्यात्मक डेटा हैं जिसके साथ कंप्यूटर संचालित होता है। पूर्णांक के लिए, दो प्रस्तुतियां हैं: हस्ताक्षरित (केवल गैर-ऋणात्मक पूर्णांक के लिए) और हस्ताक्षरित। यह स्पष्ट है कि ऋणात्मक संख्या केवल प्रतीकात्मक रूप में प्रदर्शित की जा सकती है। कंप्यूटर में इंटीजर संग्रहीत हैं निश्चित बिंदु प्रारूप.

• हस्ताक्षरित पूर्णांक प्रकारों में पूर्णांक का प्रतिनिधित्व।

  एक हस्ताक्षरित प्रतिनिधित्व के लिए, सेल के सभी अंक संख्या के प्रतिनिधित्व के लिए आवंटित किए जाते हैं। उदाहरण के लिए, एक बाइट (8 बिट्स) में, 0 से 255 तक हस्ताक्षरित संख्याओं का प्रतिनिधित्व किया जा सकता है। इसलिए, यदि यह ज्ञात है कि संख्यात्मक मान गैर-ऋणात्मक है, तो इसे बेहतर तरीके से मानना ​​बेहतर है।

  हस्ताक्षरित पूर्णांक प्रकारों में पूर्णांक का प्रतिनिधित्व।   एक हस्ताक्षरित प्रतिनिधित्व के लिए, सबसे महत्वपूर्ण (बाएं) बिट संख्या के संकेत, शेष अंकों को संख्या के लिए असाइन किया गया है। यदि संख्या सकारात्मक है, तो 0 को नकारात्मक बिट में रखा गया है, यदि ऋणात्मक - 1. उदाहरण के लिए, बाइट में, आप -128 से 127 तक हस्ताक्षरित संख्याओं का प्रतिनिधित्व कर सकते हैं।

  डायरेक्ट कोड नंबर।   सामान्य रूप "संकेत" - "मान" में एक संख्या का प्रतिनिधित्व, जिसमें सेल के उच्च-आदेश कक्ष को संकेत दिया जाता है, और शेष - द्विआधारी प्रणाली में संख्या लिखने के लिए कहा जाता है सीधा कोड बाइनरी संख्या उदाहरण के लिए, 8-बिट सेल के लिए बाइनरी संख्या 1001 और -1001 का प्रत्यक्ष कोड क्रमश: 00001001 और 10001001 है। एक कंप्यूटर में सकारात्मक संख्या हमेशा एक प्रत्यक्ष कोड का उपयोग कर प्रतिनिधित्व किया जाता है। संख्या का सीधा कोड पूरी तरह से मशीन के सेल में संख्या के रिकॉर्ड के साथ मेल खाता है। ऋणात्मक संख्या का प्रत्यक्ष कोड केवल साइन बिट की सामग्री द्वारा संबंधित सकारात्मक संख्या के प्रत्यक्ष कोड से अलग होता है। लेकिन प्रत्यक्ष पूर्णांक के माध्यम से कंप्यूटर में नकारात्मक पूर्णांक का प्रतिनिधित्व नहीं किया जाता है, तथाकथित अतिरिक्त कोड. अतिरिक्त कोड    सकारात्मक संख्या इस संख्या के प्रत्यक्ष कोड के बराबर है। ऋणात्मक संख्या मीटर का अतिरिक्त कोड 2 के - | एम | है, जहां के सेल में अंकों की संख्या है। जैसा कि पहले ही उल्लेख किया गया है, जब एक हस्ताक्षरित प्रारूप में गैर-ऋणात्मक संख्याओं का प्रतिनिधित्व करते हैं, तो सेल के सभी अंक संख्या को ही सौंपे जाते हैं। उदाहरण के लिए, एक हस्ताक्षरित प्रतिनिधित्व के साथ एक बाइट में संख्या 243 = 11110011 लिखना इस तरह दिखेगा:

एक संकेत के साथ पूर्णांक का प्रतिनिधित्व करते समय, अग्रणी (बाएं) अंक संख्या के संकेत को सौंपा गया है, और वास्तविक संख्या एक अंक कम है। इसलिए, यदि उपर्युक्त सेल स्थिति को हस्ताक्षरित पूर्णांक संख्या के रूप में माना जाता है, तो इस सेल में कंप्यूटर के लिए संख्या -13 (243 + 13 = 256 = 28) दर्ज की गई है। लेकिन यदि 16 बिट्स के सेल में एक ही नकारात्मक संख्या लिखा गया है, तो सेल की सामग्री निम्नानुसार होगी:

संख्याओं का प्रतिनिधित्व

गणित में संख्याएं

संख्या गणित की सबसे महत्वपूर्ण अवधारणा है, जो मानव इतिहास की एक लंबी अवधि में विकसित और विकसित हुई है। लोगों ने प्राचीन काल से संख्याओं के साथ काम करना शुरू किया। प्रारंभ में, एक व्यक्ति केवल सकारात्मक पूर्णांक पर संचालित होता है, जिसे प्राकृतिक संख्या कहा जाता है: 1, 2, 3, 4, ... लंबे समय तक एक राय थी कि बहुत बड़ी संख्या है, "उससे अधिक, मानव मन से परे तर्क के कारण" ।

गणितीय विज्ञान के विकास ने निष्कर्ष निकाला है कि सबसे बड़ी संख्या नहीं है। गणितीय दृष्टिकोण से, प्राकृतिक संख्याओं की श्रृंखला अनंत है, यानी। असीमित। गणित में ऋणात्मक संख्या की अवधारणा के उद्भव के साथ (आर Descartes, यूरोप में XVII शताब्दी, भारत में, बहुत पहले) यह पता चला कि पूर्णांक का सेट दोनों "बाएं" और "दाएं" असीमित है। पूर्णांक का गणितीय सेट असतत और असीमित (अनंत) है।

एक वास्तविक (या असली) संख्या की अवधारणा 18 वीं शताब्दी में इसहाक न्यूटन द्वारा गणित में पेश की गई थी। गणितीय दृष्टिकोण से वास्तविक संख्याओं का सेट अनंत और निरंतर है। इसमें कई पूर्णांक और गैर-पूर्णांक की एक और अनंत संख्या शामिल है। संख्या अक्ष पर किसी भी दो बिंदुओं के बीच वास्तविक संख्याओं का एक अनंत सेट है। वास्तविक संख्या की अवधारणा निरंतर संख्यात्मक धुरी के विचार से जुड़ी हुई है, जिसमें किसी भी बिंदु पर वास्तविक संख्या से मेल खाता है।

पूर्णांक का प्रतिनिधित्व

कंप्यूटर मेमोरी में संख्या बाइनरी नोटेशन में संग्रहीत हैं   (देखें " संख्या प्रणाली"2)। कंप्यूटर में पूर्णांक का प्रतिनिधित्व करने के लिए दो रूप हैं: हस्ताक्षरित पूर्णांक और हस्ताक्षरित पूर्णांक।

बिना हस्ताक्षर किए पूर्णांक - यह है सीमा में कई सकारात्मक संख्याएं   जहाँ कश्मीर- यह संख्या के लिए आवंटित स्मृति कक्ष की चौड़ाई है। उदाहरण के लिए, यदि 16 बिट्स (2 बाइट्स) के आकार वाले मेमोरी सेल को पूर्णांक के लिए आवंटित किया जाता है, तो उच्चतम संख्या होगी:

दशमलव नोटेशन में, यह मेल खाता है: 2 16 - 1 = 65 535

यदि सेल के सभी अंक शून्य हैं, तो यह शून्य होगा। इस प्रकार, 16-बिट सेल में 2 16 = 65 536 पूर्णांक रखे जाते हैं।

हस्ताक्षर पूर्णांक   सीमा में सकारात्मक और नकारात्मक संख्याओं का सेट है[–2   कश्मीर –1 , 2   कश्मीर   -1 - 1]। उदाहरण के लिए, कब कश्मीर   = 16 पूर्णांक की रेंज: [-32 768, 32 767]। मेमोरी सेल का उच्चतम बिट संख्या का संकेत संग्रहीत करता है: 0 एक सकारात्मक संख्या है, 1 ऋणात्मक संख्या है। सबसे बड़ा सकारात्मक संख्या 32,767 में निम्नलिखित प्रतिनिधित्व है:

उदाहरण के लिए, बाइनरी संख्या प्रणाली में स्थानांतरित होने और 16-बिट मेमोरी सेल में अंकित होने के बाद दशमलव संख्या 255, निम्नलिखित आंतरिक प्रतिनिधित्व होगा:

नकारात्मक पूर्णांक को एक अतिरिक्त कोड में दर्शाया जाता है। अतिरिक्त कोड   सकारात्मक संख्या एन   - यह है ऐसा बाइनरी प्रतिनिधित्व है, जो संख्या एन के कोड के साथ जोड़ा गया मान देता है 2   कश्मीर। यहां कश्मीर   - मेमोरी सेल में अंकों की संख्या। उदाहरण के लिए, संख्या 255 के लिए अतिरिक्त कोड निम्नानुसार है:

यह ऋणात्मक संख्या -255 का प्रतिनिधित्व है। संख्या 255 और -255 के कोड जोड़ें:

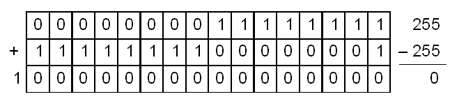
उच्च क्रम में इकाई सेल के "गिरावट", तो राशि शून्य हो गई। लेकिन यह होना चाहिए: एन + (–एन) = 0. कंप्यूटर प्रोसेसर घटाव संख्या के अतिरिक्त कोड के साथ एक अतिरिक्त के रूप में घटाव संचालन करता है। साथ ही, सेल ओवरफ़्लो (सीमा मानों से परे जा रहा है) प्रोग्राम निष्पादन में बाधा उत्पन्न नहीं करता है। इस परिस्थिति में प्रोग्रामर को पता होना चाहिए और ध्यान में रखना चाहिए!

कंप्यूटर में वास्तविक संख्याओं के प्रतिनिधित्व का प्रारूप   यह कहा जाता है फ़्लोटिंग पॉइंट प्रारूप। वास्तविक संख्या आर   एक मंटिसा के रूप में प्रस्तुत किया मीटर संख्या प्रणाली के आधार पर n   कुछ हद तक पीजिसे आदेश कहा जाता है: आर= मीटर * एन पी.

एक फ्लोटिंग पॉइंट नंबर का प्रतिनिधित्व संदिग्ध है। उदाहरण के लिए, दशमलव संख्या 25,324 के लिए, निम्न समीकरण सत्य हैं:

25.324 = 2.5324 * 10 1 = 0.0025324 * 10 4 = 2532.4 * 10 -2, आदि

अस्पष्टता से बचने के लिए, हम कंप्यूटर का उपयोग करने के लिए सहमत हुए एक फ्लोटिंग पॉइंट नंबर का सामान्यीकृत प्रतिनिधित्व। अपूर्णांश   सामान्यीकृत प्रतिनिधित्व में स्थिति को पूरा करना होगा: 0,1   n मीटर < 1   n। दूसरे शब्दों में, मंथिसा एक से कम है और पहला महत्वपूर्ण आंकड़ा शून्य नहीं है। कुछ मामलों में, सामान्यीकरण की स्थिति निम्नानुसार ली जाती है: 1   n मीटर < 10   n.

कंप्यूटर मेमोरी अपूर्णांश केवल एक महत्वपूर्ण अंकों वाले एक पूर्णांक के रूप में प्रतिनिधित्व किया   (0 पूरे और अल्पविराम संग्रहित नहीं हैं)। इसलिए, वास्तविक संख्या का आंतरिक प्रतिनिधित्व पूर्णांक की एक जोड़ी के प्रतिनिधित्व में कम हो जाता है: मंटिसा और आदेश।

विभिन्न प्रकार के कंप्यूटर संख्याओं के विभिन्न फ़्लोटिंग पॉइंट का प्रतिनिधित्व करते हैं। एक चार-बाइट मेमोरी सेल में वास्तविक संख्या के आंतरिक प्रतिनिधित्व के रूपों में से एक पर विचार करें।

सेल में संख्या के बारे में निम्नलिखित जानकारी होनी चाहिए: संख्या का संकेत, आदेश और मंटिसा के महत्वपूर्ण अंक।

प्रथम बाइट के सबसे महत्वपूर्ण बिट में संख्या का संकेत होता है: 0 का अर्थ प्लस, 1 - शून्य है। पहले बाइट के शेष 7 बिट्स में शामिल हैं मशीन ऑर्डर। अगले तीन बाइट्स मंटिसा के महत्वपूर्ण अंक (24 बिट्स) स्टोर करते हैं।

सात बाइनरी अंकों में 0000000 से 1111111 तक सीमा में बाइनरी संख्याएं रखी गईं। इसका मतलब है कि मशीन ऑर्डर 0 से 127 (दशमलव संख्या प्रणाली में) से भिन्न होता है। केवल 128 मूल्य। आदेश स्पष्ट रूप से सकारात्मक और नकारात्मक दोनों हो सकता है। आदेश के सकारात्मक और नकारात्मक मूल्यों के बीच इन 128 मानों को समान रूप से विभाजित करना उचित है: -64 से 63 तक।

मशीन ऑर्डर   गणितीय के सापेक्ष स्थानांतरित हो गया है और केवल सकारात्मक मूल्य हैं। ऑफसेट चुना जाता है ताकि आदेश का न्यूनतम गणितीय मान शून्य से मेल खाता हो।

इस मामले में मशीन ऑर्डर (एमपी) और गणितीय (पी) के बीच संबंध सूत्र द्वारा व्यक्त किया गया है: एमपी = पी +64।

परिणामी सूत्र दशमलव में लिखा गया है। बाइनरी सिस्टम में, सूत्र है: एमपी 2 = पी 2 + 100 0000 2।

वास्तविक संख्या के आंतरिक प्रतिनिधित्व को रिकॉर्ड करने के लिए, आपको यह करना होगा:

1) किसी दिए गए नंबर के मॉड्यूल को 24 महत्वपूर्ण अंकों के साथ बाइनरी संख्या प्रणाली में अनुवादित करें,

2) द्विआधारी संख्या को सामान्य करें,

3) द्विआधारी संख्या प्रणाली में मशीन ऑर्डर पाएं,

4) एक संख्या के संकेत को ध्यान में रखते हुए, चार-बाइट मशीन शब्द में इसका प्रतिनिधित्व लिखें।

एक उदाहरणफ्लोटिंग पॉइंट फॉर्म में 250.1875 की आंतरिक प्रतिनिधित्व लिखें।

  निर्णय

1. इसे 24 महत्वपूर्ण अंकों के साथ एक बाइनरी संख्या प्रणाली में अनुवाद करें:

250,1875 10 = 11111010,0011000000000000 2 .

2. सामान्यीकृत बाइनरी फ़्लोटिंग पॉइंट नंबर के रूप में लिखें:

0.111110100011000000000000 एच 10 2 1000।

यहां मंथिसा है, जो संख्या प्रणाली का आधार है
  (2 10 = 10 2) और ऑर्डर (8 10 = 1000 2) बाइनरी सिस्टम में लिखे गए हैं।

3. बाइनरी संख्या प्रणाली में मशीन ऑर्डर की गणना करें:

एमपी 2 = 1000 + 100 0000 = 100 1000।

4. हम संख्या के संकेत को ध्यान में रखते हुए, चार-बाइट मेमोरी सेल में किसी संख्या का प्रतिनिधित्व लिखते हैं

हेक्साडेसिमल फॉर्म: 48FA3000।

वास्तविक संख्याओं की सीमा पूर्णांक की सीमा से कहीं अधिक व्यापक है। सकारात्मक और नकारात्मक संख्याओं को समरूप रूप से शून्य के बारे में व्यवस्थित किया जाता है। नतीजतन, अधिकतम और न्यूनतम संख्या मॉड्यूलस में एक-दूसरे के बराबर होती है।

पूर्ण मूल्य में सबसे छोटा शून्य है। पूर्ण मूल्य फ्लोटिंग प्वाइंट फॉर्म में सबसे बड़ा सबसे बड़ा मंटिसा और सबसे बड़ा ऑर्डर वाला नंबर है।

चार बाइट मशीन शब्द के लिए, ऐसी संख्या होगी:

0.111111111111111111111111 · 10 21111111।

दशमलव संख्या प्रणाली में स्थानांतरण के बाद हमें मिलता है:

MAX = (1 - 2 -24) · 2 63 10 1 9।

यदि, वास्तविक संख्याओं के साथ गणना में, परिणाम स्वीकार्य सीमा के बाहर है, तो प्रोग्राम का निष्पादन बाधित है।   ऐसा होता है, उदाहरण के लिए, शून्य से विभाजित होने पर, या बहुत छोटी संख्या से, शून्य के करीब।

वास्तविक संख्या जिनकी मंथिसा की बिट गहराई स्मृति कोशिका में मंटिसा के लिए आवंटित अंकों की संख्या से अधिक है, कंप्यूटर में लगभग ("फसल" मंटिसा के साथ) का प्रतिनिधित्व किया जाता है। उदाहरण के लिए, कंप्यूटर में 0.1 की एक तर्कसंगत दशमलव संख्या लगभग (गोलाकार) का प्रतिनिधित्व किया जाएगा, क्योंकि द्विआधारी संख्या प्रणाली में इसकी मंटिसा की संख्या असीमित संख्या है। इस निकटता का परिणाम वास्तविक संख्याओं के साथ मशीन गणनाओं की त्रुटि है।

असली संख्या कंप्यूटर के साथ गणना लगभग प्रदर्शन करता है। ऐसी गणनाओं की त्रुटि कहा जाता हैमशीन गोलाकार त्रुटि.

वास्तविक संख्याओं का सेट, जो फ्लोटिंग पॉइंट के रूप में कंप्यूटर मेमोरी में सटीक रूप से प्रतिनिधित्व योग्य है, सीमित और अलग है। विवेकपूर्णता ऊपर वर्णित अनुसार, मंटिसा के सीमित अंकों के परिणाम का परिणाम है।

वास्तविक संख्याओं की संख्या, जो कंप्यूटर की स्मृति में बिल्कुल प्रतिनिधित्व करने योग्य है, को सूत्र द्वारा गणना की जा सकती है: एन = 2   टी · ( यू – एल   + 1) + 1. यहां टी - मंटिसा के बाइनरी अंकों की संख्या; यू   - गणितीय क्रम का अधिकतम मूल्य; एल   - आदेश का न्यूनतम मूल्य। उपर्युक्त प्रस्तुति विकल्प के लिए ( टी = 24, यू = 63,
  एल   = -64) प्राप्त किया जाता है: एन = 2 146 683 548.

उदाहरण 1दो-बाइट मेमोरी सेल में पूर्णांक 1607 के "हस्ताक्षरित" प्रारूप में आंतरिक प्रतिनिधित्व प्राप्त करें।

निर्णय

1) संख्या को बाइनरी संख्या प्रणाली में स्थानांतरित करें: 1607 10 = 11001000111 2।

2) बाईं ओर 16 बिट्स तक शून्य लिखना, हमें सेल में इस संख्या का आंतरिक प्रतिनिधित्व मिलता है:

यह दिखाने के लिए वांछनीय है कि हेक्साडेसिमल फॉर्म का उपयोग इस कोड को लिखने के संपीड़ित रूप के लिए कैसे किया जाता है, जिसे प्रत्येक चार बाइनरी संख्याओं को एक हेक्साडेसिमल संख्या: 0647 के साथ बदलकर प्राप्त किया जाता है (देखें " संख्या प्रणाली” 2).

एक नकारात्मक पूर्णांक के आंतरिक प्रतिनिधित्व प्राप्त करने का कार्य अधिक कठिन है (- एन) - अतिरिक्त कोड। हमें छात्रों को इस प्रक्रिया के एल्गोरिदम दिखाने की जरूरत है:

1) एक सकारात्मक संख्या का आंतरिक प्रतिनिधित्व प्राप्त करें एन;

2) 0 को 1 और 1 के साथ 0 के साथ बदलकर इस नंबर का रिवर्स कोड प्राप्त करें;

3) परिणामी संख्या 1 में जोड़ें।

उदाहरण 2दो-बाइट मेमोरी सेल में एक पूर्ण ऋणात्मक संख्या -1607 का आंतरिक प्रतिनिधित्व प्राप्त करें।

निर्णय

यह छात्रों को दिखाने के लिए उपयोगी है कि छोटे नकारात्मक संख्या का आंतरिक प्रतिनिधित्व कैसे दिखता है। डबल-बाइट सेल में, यह -32,768 है।

1) 32 768 = 2 15 के बाद, संख्या 32 768 को द्विआधारी संख्या प्रणाली में अनुवाद करना आसान है। इसलिए, द्विआधारी प्रणाली में यह है:

2) हम रिवर्स कोड लिखते हैं:

3) इस बाइनरी नंबर में एक जोड़ें, हमें मिलता है

पहले बिट में से एक ऋण चिह्न इंगित करता है। यह सोचने की कोई आवश्यकता नहीं है कि परिणामी कोड शून्य से शून्य है। यह एक अतिरिक्त कोड के रूप में -32,768 है। ये पूर्णांक के मशीन प्रतिनिधित्व के लिए नियम हैं।

इस उदाहरण को दिखाते हुए, छात्रों को स्वतंत्र रूप से साबित करना है कि 32767 + (-32 768) के कोड जोड़ने के परिणामस्वरूप संख्या -1 का कोड होगा।