Ako propagovať skupinu v Odnoklassniki sami: pokyny krok za krokom
Ako propagovať predajnú stránku na Odnoklassniki nezávisle a zadarmo, ako aj platené možnosti ...
Závislosť jednej premennej od druhej sa nazýva funkčná závislosť. Variabilná závislosť r z premennej X volal funkciu, ak každá hodnota X sa zhoduje s jednou hodnotou r.
Označenie:
premenlivý X nazývaná nezávislá premenná resp argument a premenná r- závislý. To hovoria r je funkciou X. Význam r zodpovedajúce danej hodnote X, volal funkčná hodnota.
Všetky hodnoty, ktoré si vyžaduje X, formulár rozsah funkcie; všetky hodnoty, ktoré si vyžaduje r, formulár súbor funkčných hodnôt.
Označenia: 
D(f)- hodnoty argumentov. E(f)- funkčné hodnoty. Ak je funkcia daná vzorcom, predpokladá sa, že oblasť definície pozostáva zo všetkých hodnôt premennej, pre ktoré má tento vzorec zmysel.
Graf funkcií volá sa množina všetkých bodov na súradnicovej rovine, ktorých úsečky sa rovnajú hodnotám argumentu a súradnice sa rovnajú zodpovedajúcim hodnotám funkcie. Ak nejakú hodnotu x=x0 porovnať viacero hodnôt (nie iba jednu) r, potom takáto korešpondencia nie je funkciou. Na to, aby množina bodov súradnicovej roviny bola grafom nejakej funkcie, je potrebné a postačujúce, aby sa ľubovoľná priamka rovnobežná s osou Oy pretínala s grafom najviac v jednom bode.

1) Funkciu je možné nastaviť analyticky vo forme vzorca. napr. ![]()
2) Funkcia môže byť definovaná tabuľkou mnohých párov (x; y).
3) Funkciu je možné nastaviť graficky. Hodnotové páry (x; y) zobrazené na súradnicovej rovine.
Funkcia f(x) volal zvyšujúci sa na danom číselnom intervale, ak väčšia hodnota argumentu zodpovedá väčšej hodnote funkcie. Predstavte si, že sa určitý bod pohybuje po grafe zľava doprava. Potom sa bod akosi „vyšplhá“ hore v tabuľke.
Funkcia f(x) volal ubúdanie na danom číselnom intervale, ak väčšia hodnota argumentu zodpovedá menšej hodnote funkcie. Predstavte si, že sa určitý bod pohybuje po grafe zľava doprava. Potom sa bod akoby „zroloval“ v tabuľke.
Volá sa funkcia, ktorá na danom číselnom intervale iba rastie alebo len klesá monotónna na tomto intervale.

hodnoty X, na ktorom y=0, sa volá funkčné nuly. Sú to úsečky priesečníkov grafu funkcie s osou x.

Takéto rozsahy hodnôt X, na ktorom sú hodnoty funkcie r buď len pozitívne alebo len negatívne sa nazývajú intervaly znamienkovej stálosti funkcie.

Dokonca aj funkcia
1) Definičný obor je symetrický vzhľadom na bod (0; 0), teda ak bod a patrí do oblasti definície, potom pointa -a patrí tiež do oblasti definície.
2) Za akúkoľvek hodnotu X f(-x)=f(x)
3) Graf párnej funkcie je symetrický okolo osi Oy.
nepárna funkcia má nasledujúce vlastnosti:
1) Definičný obor je symetrický vzhľadom na bod (0; 0).
2) pre akúkoľvek hodnotu X, ktorá patrí do oblasti definície, rovnosti f(-x)=-f(x)
3) Graf nepárnej funkcie je symetrický vzhľadom na počiatok (0; 0).
Nie každá funkcia je párna alebo nepárna. Funkcie všeobecný pohľad nie sú párne ani nepárne.



Funkcia f sa nazýva periodické, ak existuje číslo také, že pre ľubovoľné X z oblasti definície rovnosti f(x)=f(x-T)=f(x+T). T je obdobie funkcie.
Každá periodická funkcia má nekonečný počet periód. V praxi sa zvyčajne berie do úvahy najmenšie pozitívne obdobie.
Hodnoty periodickej funkcie sa opakujú po intervale, ktorý sa rovná perióde. Používa sa pri vykresľovaní grafov.

D(f)- tie hodnoty, ktoré môže nadobudnúť argument, t.j. rozsah funkcie.
E(f)- tie hodnoty, ktoré funkcia môže nadobudnúť, t.j. súbor funkčných hodnôt.
postupné zisťovanie hodnôt argumentov zložitých funkcií;
bodovacia/hraničná metóda;
využitie vlastností spojitosti a monotónnosti funkcie;
použitie derivátu;
použitie najväčších a najmenších hodnôt funkcie;
grafická metóda;
metóda zavádzania parametrov;
metóda inverznej funkcie.
Uvažujme o niektorých z nich.
Všeobecný prístup nájsť množinu hodnôt spojitej funkcie f(x) znamená nájsť najväčšiu a najmenšiu hodnotu funkcie f(x) v jej doméne (alebo dokázať, že jedna alebo obe neexistujú) .
Ak potrebujete nájsť množinu hodnôt funkcie na segmente:
nájdite deriváciu danej funkcie f "(x);
nájdite kritické body funkcie f(x) a vyberte tie, ktoré patria do daného segmentu;
vypočítajte hodnoty funkcie na koncoch segmentu a vo vybraných kritických bodoch;
spomedzi nájdených hodnôt vyberte najmenšiu a najväčšiu hodnotu;
Medzi týmito hodnotami sa uzatvára množina funkčných hodnôt.
Ak je rozsah funkcie interval, potom sa použije rovnaká schéma, ale namiesto hodnôt na koncoch sa použijú limity funkcie, keď argument smeruje ku koncom intervalu. Limitné hodnoty od nie sú zahrnuté v súbore hodnôt.
Ak chcete nájsť množinu funkčných hodnôt, najskôr nájdite množinu hodnôt argumentov a potom nájdite zodpovedajúce minimálne a maximálne hodnoty funkčnej funkcie. Pomocou nerovností – určte hranice.
Podstatou je odhadnúť spojitú funkciu zdola a zhora a dokázať, že funkcia dosahuje dolnú a hornú hranicu odhadov. V tomto prípade je zhoda množiny hodnôt funkcie s intervalom od dolnej hranice odhadu po hornú určená kontinuitou funkcie a absenciou iných hodnôt.
Ďalšou možnosťou je transformovať funkciu na spojitú monotónnu funkciu, následne pomocou vlastností nerovností odhadnúť množinu hodnôt novo získanej funkcie.
Na základe postupného vyhľadávania množiny hodnôt medziľahlých funkcií, ktoré tvoria funkciu
| Funkcia | Veľa hodnôt |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^(2n)$ | E(y) = |
| $y = \cos(x)$ | E(y) = [-1;1] |
| $y = (\rmtg)\, x$ | E(y) = (-∞;+∞) |
| $y = (\rm ctg)\, x$ | E(y) = (-∞;+∞) |
| $y = \arcsin(x)$ | E(y) = [-π/2; π/2] |
| $y = \arccos(x)$ | E(y) = |
| $y = (\rm arctg)\, x$ | E(y) = (-π/2; π/2) |
| $y = (\rm arcctg)\, x$ | E(y) = (0; π) |
Nájdite množinu funkčných hodnôt:
Nájdite definičný obor: D(f)=[-3;3], pretože $9-x^(2)\geq 0$
Nájdite derivát: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$
f"(x) = 0, ak x = 0. f"(x) neexistuje, ak $\sqrt(9-x^(2))=0$, t. j. pre x = ±3. Získame tri kritické body: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, z ktorých dva sa zhodujú s koncami segmentu. Vypočítajte: f(–3) = 0, f(0) = 3, f(3) = 0. Najmenšia hodnota f(x) je teda 0, najväčšia hodnota je 3.
Odpoveď: E(f) = .
Nájdite najväčšie a najmenšie hodnoty funkcie:
Od $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $, potom:
$f(x)\leq \frac(3)(4)$ pre všetky x;
$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ pre všetky x(pretože $|\cos (x)|\leq 1$);
$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;
$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;
Odpoveď: $\frac(3)(4)$ a $-\frac(3)(2)$
Ak tento problém vyriešite pomocou derivácií, potom budete musieť prekonať prekážky spojené s tým, že funkcia f (x) nie je definovaná na úsečke, ale na celej reálnej čiare.
Z definície sínusu vyplýva, že $-1\leq\sin(x)\leq 1$. Ďalej využívame vlastnosti číselných nerovností.
$-4\leq - 4\sin(x)\leq 4$, (vynásobte všetky tri časti dvojitej nerovnosti -4);
$1\leq 5 - 4\sin(x)\leq 9$ (pripočítané k trom častiam dvojitej nerovnosti 5);
Keďže táto funkcia je spojitá v celej oblasti definície, množina jej hodnôt leží medzi jej najmenšou a najväčšou hodnotou v celej oblasti definície, ak existuje.
V tomto prípade je množinou hodnôt funkcie $y = 5 - 4\sin(x)$ množina .
Z nerovností $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ získame odhad $$\\ -6\leq y\ leq 6 $ $
Pre x = p a x = 0 má funkcia hodnoty -6 a 6, t.j. dosahuje dolnú a hornú hranicu. Ako lineárna kombinácia spojitých funkcií cos(7x) a cos(x) je funkcia y spojitá pozdĺž celej číselnej osi, takže vlastnosťou spojitej funkcie nadobúda všetky hodnoty od -6 do 6 vrátane a iba oni, keďže kvôli nerovnostiam $- 6\leq y\leq 6$ iné hodnoty nie sú pre ňu možné.
Preto E(y) = [-6;6].
$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Odpoveď: E(f) = .
$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].
$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .
Transformujme výraz $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \vpravo) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.
Definícia kosínusu znamená $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$
Keďže táto funkcia je spojitá na celej doméne definície, potom je množina jej hodnôt uzavretá medzi jej najmenšou a najväčšou hodnotou, ak existuje, množinou hodnôt funkcie $y =\sqrt(2)\ cos((x +\frac(\pi)(4)))$ je množina $[-\sqrt(2);\sqrt(2)]$.
$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$
Označte $t = 5 – (3^(x)+1)^(2)$, kde -∞≤t≤4. Problém sa teda redukuje na nájdenie množiny hodnôt funkcie $y = \log_(0,5)(t)$ na lúči (-∞;4). Keďže funkcia $y = \log_(0,5)(t)$ je definovaná len pre t > 0 , jej množina hodnôt na lúči (-∞;4) sa zhoduje s množinou hodnôt funkcia na intervale (0;4), ktorá predstavuje priesečník lúča (-∞;4) s definičným oborom (0;+∞) logaritmickej funkcie. Na intervale (0;4) je táto funkcia spojitá a klesajúca. Pre t > 0 má tendenciu k +∞ a pre t = 4 nadobúda hodnotu -2, teda E(y) = (-2, +∞).
Používame techniku založenú na grafickom znázornení funkcie.
Po transformáciách funkcie máme: y 2 + x 2 = 25 a y ≥ 0, |x| ≤ 5.
Treba pripomenúť, že $x^(2)+y^(2)=r^(2)$ je rovnica kruhu s polomerom r.
Pri týchto obmedzeniach je grafom tejto rovnice horný polkruh so stredom v počiatku a polomer rovný 5. Je zrejmé, že E(y) = .
Odpoveď: E(y) = .
Rozsah funkcií v úlohách jednotnej štátnej skúšky, Minyuk Irina Borisovna
Tipy na nájdenie množiny funkčných hodnôt, Belyaeva I., Fedorova S.
Nájdenie množiny funkčných hodnôt
Ako riešiť problémy z matematiky na prijímacích skúškach, I.I. Melnikov, I.N. Sergeev
Dnes sa v lekcii budeme venovať jednému zo základných pojmov matematiky – pojmu funkcie; Pozrime sa bližšie na jednu z vlastností funkcie – množinu jej hodnôt.
Počas vyučovania
učiteľ. Pri riešení problémov si všimneme, že niekedy je to práve nájdenie množiny hodnôt funkcie, ktoré nás dostáva do zložitých situácií. prečo? Zdalo by sa, že pri štúdiu funkcie od 7. ročníka o nej vieme veľa. Preto máme všetky dôvody na preventívny krok. Poďme sa dnes „hrať“ s množstvom funkčných hodnôt, aby sme vyriešili mnohé z otázok na túto tému v nadchádzajúcej skúške.
Množiny hodnôt elementárnych funkcií
učiteľ. Na začiatok je potrebné zopakovať grafy, rovnice a množiny hodnôt základných elementárnych funkcií v celej oblasti definície.
Na obrazovke sa premietajú grafy funkcií: lineárne, kvadratické, zlomkovo-racionálne, trigonometrické, exponenciálne a logaritmické, pre každú z nich je verbálne určená množina hodnôt. Venujte pozornosť skutočnosti, že lineárna funkcia E(f) = R alebo jedno číslo pre lineárne zlomky
Toto je naša abeceda. Pridaním našich znalostí o transformáciách grafov: paralelný preklad, naťahovanie, stláčanie, odraz, môžeme vyriešiť problémy prvej časti POUŽÍVAŤ a ešte trochu ťažšie. Poďme si to overiť.
Samostatná práca
o slová úlohy a súradnicové systémy vytlačené pre každého študenta.
1. Nájdite množinu funkčných hodnôt v celej doméne definície:
a) r= 3 hriechy X ;
b) r = 7 – 2 X
;
v) r= -arccos( X + 5):
G) r= | arctg X |;
e)
2. Nájdite množinu funkčných hodnôt r = X 2 medzi tým J, ak:
a) J = ;
b) J = [–1; 5).
3. Definujte funkciu analyticky (rovnicou), ak množina jej hodnôt:
1) E(f(X)) = (–∞ ; 2] a f(X) - funkcia
štvorec
b) logaritmické,
c) demonštratívne;
2) E(f(X)) = R \{7}.
Pri diskusii o úlohe 2samostatnej práce upozorniť žiakov na to, že v prípade monotónnosti a nadväznosti funkcie y=f(X)v danom intervale[a;b],súbor jeho významov-medzera,ktorých koncami sú hodnoty f(a)a f(b).
Možnosti odpovede pre úlohu 3.
1.
a) r = –X 2 + 2 , r = –(X
+ 18) 2 + 2,
r= a(X – X c) 2 + 2 at a < 0.
b) r= -| denník 8 X | + 2,
v) r = –| 3 X – 7 | + 2, r = –5 | X | + 3.
2.
a) b)
v) r = 12 – 5X, kde X ≠ 1 .
Nájdenie množiny hodnôt funkcie pomocou derivácie
učiteľ. V 10. ročníku sme sa zoznámili s algoritmom hľadania extrémov funkcie spojitej na segmente a hľadania jej množiny hodnôt bez spoliehania sa na graf funkcie. Pamätáte si, ako sme to urobili? ( S pomocou derivátu.) Pripomeňme si tento algoritmus .
1. Skontrolujte funkciu r = f(X) je definovaný a spojitý na intervale J = [a; b]. 2. Nájdite hodnoty funkcií na koncoch segmentu: f(a) a f(b). Komentujte. Ak vieme, že funkcia je spojitá a monotónna J, potom môžete okamžite odpovedať: E(f) = [f(a); f(b)] alebo E(f) = [f(b); f(a)]. 3. Nájdite deriváciu a potom kritické body x kJ. 4. Nájdite funkčné hodnoty v kritických bodoch f(x k). 5. Porovnajte funkčné hodnoty f(a), f(b) a f(x k), vyberte najväčšiu a najmenšiu hodnotu funkcie a odpovedzte: E(f)= [f prenájom; f naíb]. |
Úlohy na aplikáciu tohto algoritmu sa nachádzajú vo variantoch skúšky. Napríklad v roku 2008 bola takáto úloha navrhnutá. Musíte to vyriešiť Domy .
Úloha C1. Nájdite najväčšiu hodnotu funkcie
f(X) = (0,5X + 1) 4 – 50(0,5X + 1) 2
v | X + 1| ≤ 3.
Podmienky domácej úlohy vytlačené pre každého študenta .
Nájdenie množiny hodnôt komplexnej funkcie
učiteľ. Hlavnou časťou našej lekcie budú neštandardné úlohy obsahujúce zložité funkcie, ktorých deriváty sú veľmi zložité výrazy. A grafy týchto funkcií sú nám neznáme. Preto na riešenie použijeme definíciu komplexnej funkcie, teda závislosť medzi premennými v poradí ich vnorenia do tejto funkcie a posúdenie ich rozsahu (intervalu zmeny ich hodnôt). Problémy tohto typu sa nachádzajú v druhej časti skúšky. Obráťme sa na príklady.
Cvičenie 1. Pre funkcie r = f(X) a r = g(X) napíšte komplexnú funkciu r = f(g(X)) a nájdite jeho množinu hodnôt:
a) f(X) = –X 2 + 2X +
3, g(X) = hriech X;
b) f(X) = –X 2 + 2X +
3, g(X) = log 7 X;
v)
g(X) = X 2 + 1;
G)
Riešenie. a) Komplexná funkcia má tvar: r= hriech 2 X+2 hriech X + 3.
Uvádzame prechodný argument t, môžeme túto funkciu napísať takto:
r= –t 2 + 2t+ 3, kde t= hriech X.
Pri vnútornej funkcii t= hriech X argument má akúkoľvek hodnotu a množinou jeho hodnôt je segment [–1; jeden].
Takže pre vonkajšiu funkciu r = –t 2 +2t+ 3 sme sa naučili interval zmeny hodnôt jeho argumentu t: t[-jeden; jeden]. Pozrime sa na graf funkcie r = –t 2 +2t + 3.

Všimnite si, že kvadratická funkcia pre t[-jeden; 1] má na koncoch najmenšie a najväčšie hodnoty: r najímanie = r(–1) = 0 a r naib = r(1) = 4. A keďže táto funkcia je spojitá na intervale [–1; 1], potom preberá aj všetky hodnoty medzi nimi.
Odpoveď: r .
b) Zloženie týchto funkcií nás vedie ku komplexnej funkcii, ktorú po zavedení medziargumentu možno znázorniť takto:
r= –t 2 + 2t+ 3, kde t= denník 7 X,

Funkcia t= denník 7 X
X (0; +∞ ), t (–∞ ; +∞ ).
Funkcia r = –t 2 + 2t+ 3 (pozri graf) argument t má akúkoľvek hodnotu a samotná kvadratická funkcia má všetky hodnoty nie väčšie ako 4.
Odpoveď: r (–∞ ; 4].
c) Komplexná funkcia má nasledujúci tvar:

Zavedením stredného argumentu dostaneme:
kde t = X 2 + 1.
Keďže pre vnútornú funkciu X R , a t .
Odpoveď: r (0; 3].
d) Zloženie týchto dvoch funkcií nám dáva komplexnú funkciu
ktoré možno napísať ako

Všimni si
Takže, o
kde k Z , t [–1; 0) (0; 1].
Kreslenie grafu funkcie vidíme to pri týchto hodnotách t
r(–∞ ; –4] c ;
b) v celej oblasti definície.
Riešenie. Najprv preskúmame monotónnosť tejto funkcie. Funkcia t= arcctg X- nepretržitý a klesajúci na R a množina jeho hodnôt (0; π). Funkcia r= log 5 t je definovaný na intervale (0; π), je spojitý a na ňom rastie. To znamená, že táto komplexná funkcia na súprave klesá R . A ako zloženie dvoch spojitých funkcií bude spojité ďalej R .
Poďme vyriešiť problém "a".
Keďže funkcia je spojitá na celej číselnej osi, je spojitá na ktorejkoľvek jej časti, najmä na danom segmente. A potom v tomto segmente má najmenšie a najväčšie hodnoty a preberá všetky hodnoty medzi nimi:
Ktorá z výsledných hodnôt je väčšia? prečo? A aký bude súbor hodnôt?
odpoveď: ![]()
Poďme vyriešiť problém "b".

odpoveď: pri(–∞ ; log 5 π) v celej oblasti definície.
Úloha s parametrom
Teraz skúsme zostaviť a vyriešiť jednoduchú rovnicu s parametrom tvaru f(X) = a, kde f(X) - rovnaká funkcia ako v úlohe 4.
Úloha 5. Určte počet koreňov log 5 rovnice (arcctg X) = a pre každú hodnotu parametra a.
Riešenie. Ako sme už ukázali v úlohe 4, funkcia pri= log 5 (arctg X) klesá a stále pokračuje R a nadobúda hodnoty menšie ako log 5 π. Tieto informácie stačia na odpoveď.
odpoveď: ak a < log 5 π, то уравнение имеет единственный корень;
ak a≥ log 5 π, potom neexistujú žiadne korene.
učiteľ. Dnes sme zvážili problémy súvisiace s nájdením množiny funkčných hodnôt. Na tejto ceste sme objavili novú metódu riešenia rovníc a nerovníc - metódu odhadu, takže hľadanie množiny hodnôt funkcie sa stalo prostriedkom na riešenie problémov vyššej úrovne. Zároveň sme videli, ako sa takéto problémy konštruujú a ako monotónne vlastnosti funkcie uľahčujú ich riešenie.
A rád by som dúfal, že logika, ktorá spájala dnes zvažované úlohy, vás prekvapila, alebo aspoň prekvapila. Nemôže to byť inak: výstup na nový vrchol nenechá nikoho ľahostajným! Všímame si a oceňujeme krásne obrazy, sochy atď. Ale aj matematika má svoju krásu, príťažlivú a očarujúcu – krásu logiky. Matematici hovoria, že krásne riešenie je zvyčajne správne riešenie a nie je to len fráza. Teraz musíte sami nájsť takéto riešenia a my sme dnes naznačili jednu z ciest k nim. Veľa šťastia! A pamätajte: cestu zvládne ten kráčajúci!
lýceum GBOU (hospodárske) s. Isakla

Učiteľka matematiky Kuzaeva V.N.
2016
Referenčné materiály
Ukážka riešenia Nájdite množinu funkčných hodnôt

Rozsah funkcie  je
je
r - ľubovoľné číslo
Rozsah funkcie  je
je





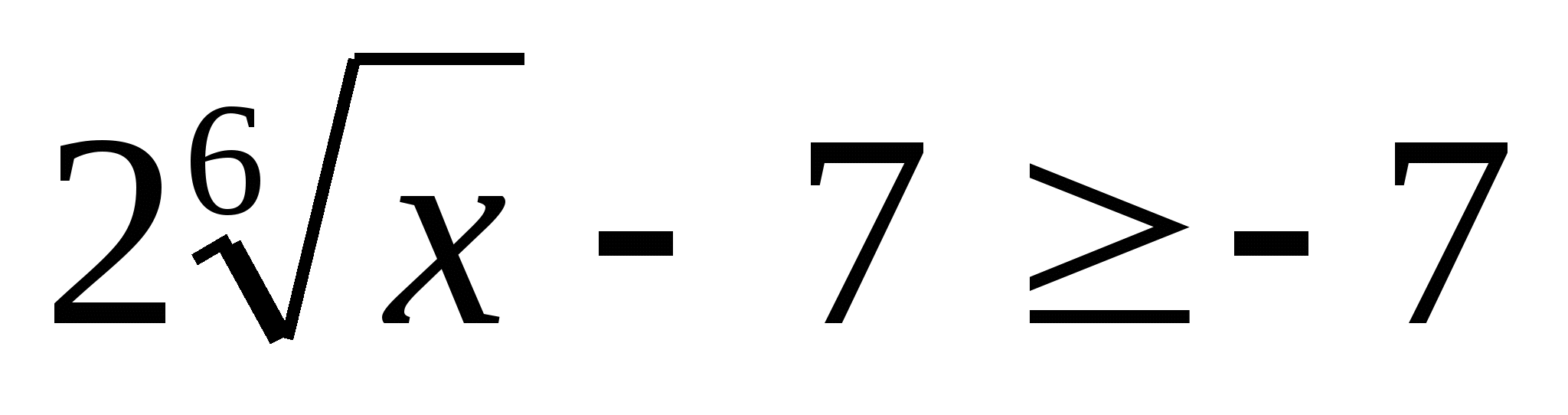
Veľa hodnôt

r - ľubovoľné číslo


Najvyššia hodnota
Najnižšia hodnota



doména X
- ľubovoľné číslo  , kde
, kde 
 , kde
, kde 
Veľa hodnôt 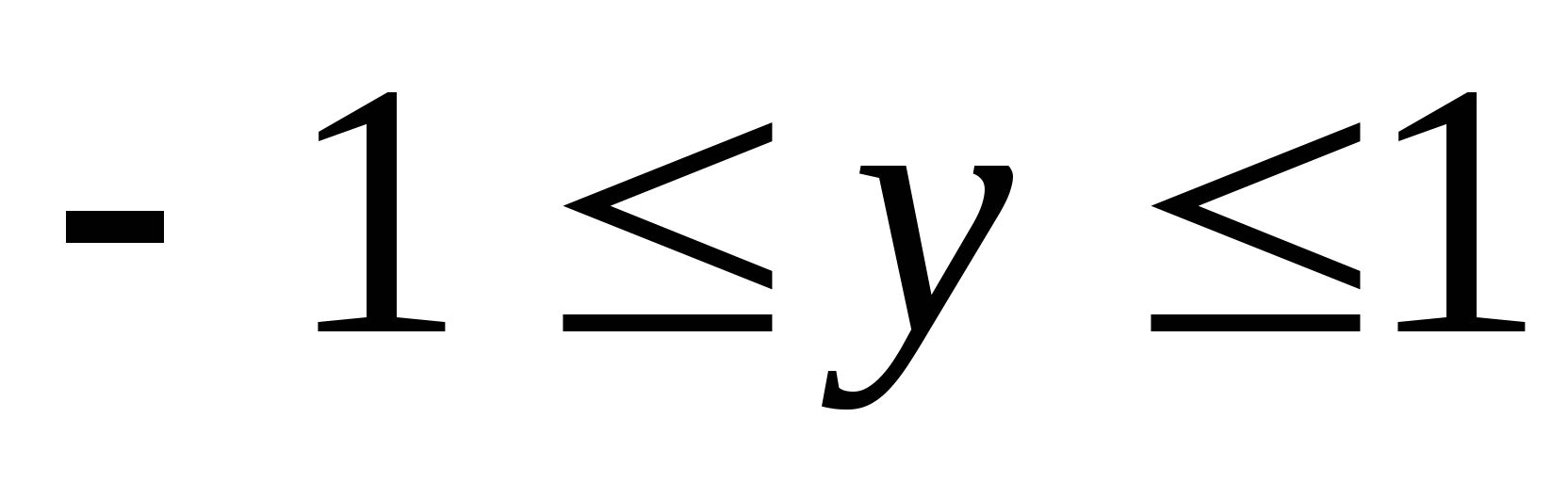 r
- ľubovoľné číslor
- ľubovoľné číslo
r
- ľubovoľné číslor
- ľubovoľné číslo
Vykresľovanie šablón pre niektoré goniometrické funkcie
Sada hodnôt goniometrických funkcií
možnosť 1
Y =
hriech 3x+2.1) (-5;5) 2) 3) 4) (1;5)
2. Nájdite oblasť funkcie y =tg x + 1.
1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2
4. Zadajte najmenšie celé číslo z rozsahu funkcie
y = 12,7 + 5 hriech(3x-2).
1) -5 2) 8 3) 5 4) 17
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-2;2].
1) y = cos 2x 2) y = hriech 2 X 3) r = cos 2 X +2
4) r = 2 hriech 4 X
6. Nájdite množinu funkčných hodnôtr =
tg 2
Xna segmente 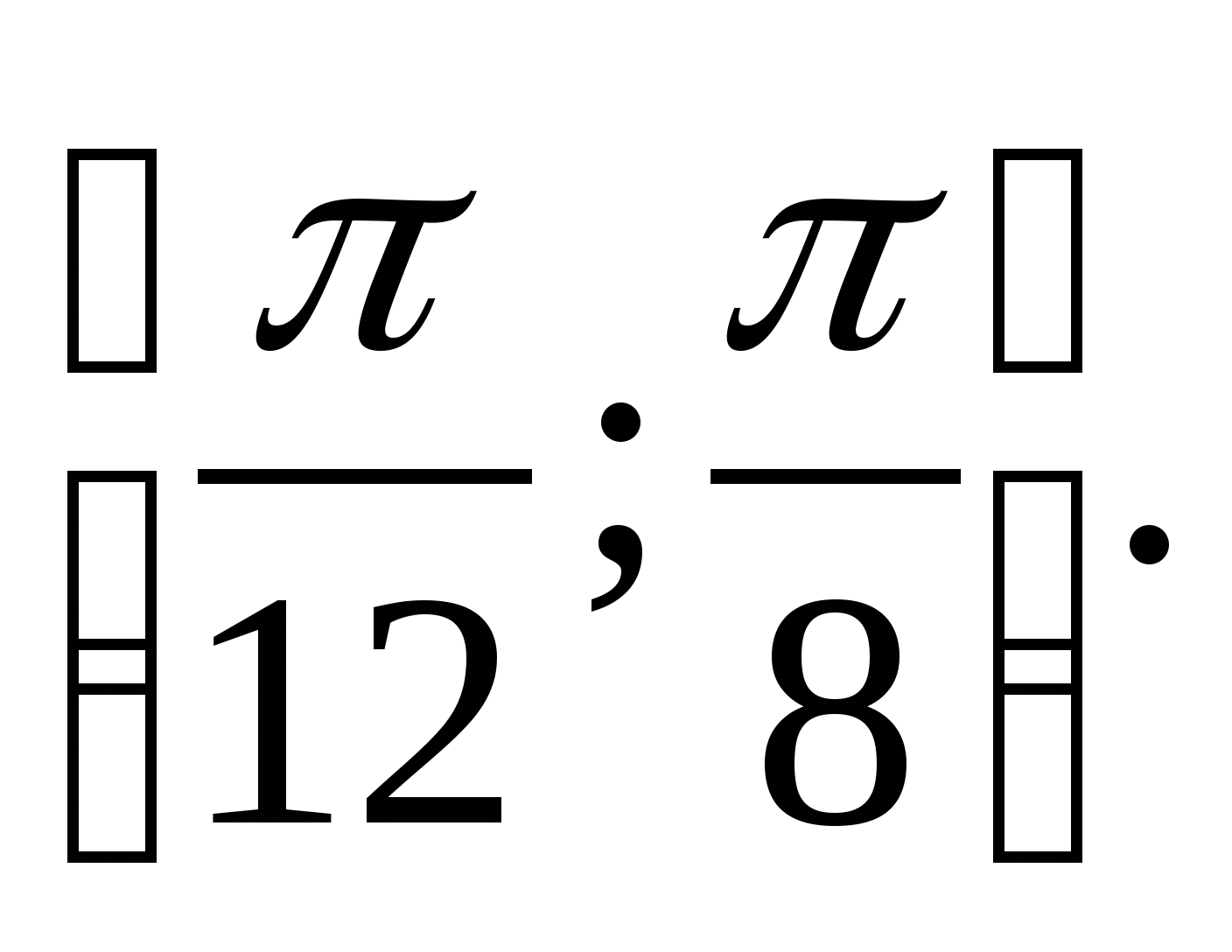




7. Nájdite súčet všetkých celých čísel, ktoré sú v rozsahu funkcier = 4 cos 2 X – 7.
1) -25 2) 25 3) -22 4) 0
Možnosť 2
r = 2 cos 5 X +3.
1) (2;3) 2) 3) (1;5) 4) .
2. Nájdite rozsah funkcie 
1) 3) (-∞;∞) 4) .
3. Zadajte najmenšie číslo z rozsahu funkcie

1) 4 2) -3 3) 1 4) -7
4. Zadajte najväčšie celé číslo z rozsahu funkcie

1) 2 2) 13 3) 12 4) -2
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-5;5].
1) y = hriech 5x 2) y = 5 cos 5x 3) y = cos (-5x)
4) y = hriech 5x + 5
6. Nájdite množinu funkčných hodnôt  na segmente
na segmente 




7. Nájdite súčin všetkých celých čísel, ktoré sú v rozsahu funkcie y \u003d 5 – 3hriech 2 X.
1) 120 2) 14 3) -15 4) 0
Možnosť 3
1. Zadajte množinu funkčných hodnôtr =
hriech 3
X + 5.
1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)
3. Zadajte najmenšie číslo z rozsahu funkcie y = 5tg 2 X+2?
1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3
5. Zadajte funkciu, ktorej množinou hodnôt je segment
[-17;-13].
1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15
2) y = 2 cos x - 15 4) y = 3 hriechy x +10
6. Uveďte najmenšie prirodzené číslo, ktoré nie je zahrnuté v množine funkčných hodnôt 
1) 2 2) 4 3) 15 4) 6
7. Koľko celých čísel patrí do množiny funkčných hodnôt
r = 2 cos 3 X +10?
1) 2 2) 3 3) 4 5) 5
Možnosť 4
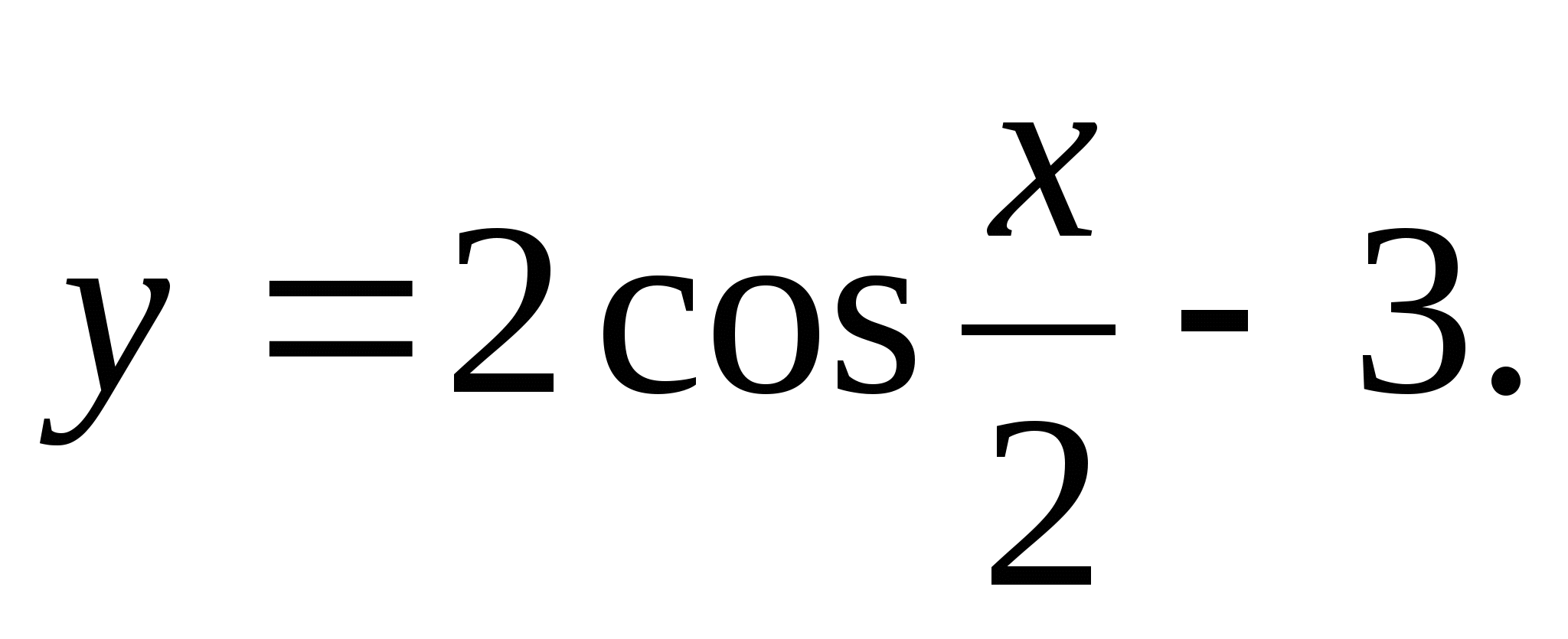
1) 2) 4) (-7;-6)
2. Nájdite rozsah funkcie 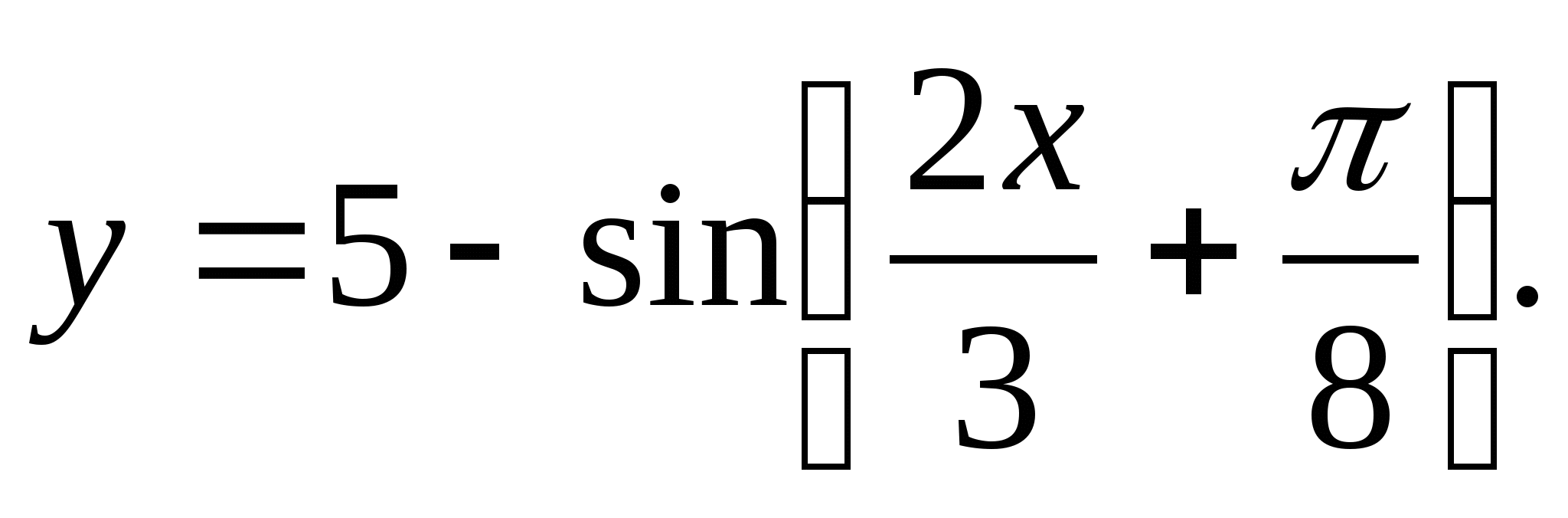
1) (1;5) 2) 3) (4;6) 4) [-6;-4]
3. Zadajte najväčšie číslo z rozsahu funkcier = -3 ctg 2 X+7.
1) 10 2) 4 3) 7 4) -3
4. Ktoré z nasledujúcich čísel nie je zahrnuté v množine funkčných hodnôt 
1) -6 2) -5 3) -10 4) -7
5. Zadajte funkciu, ktorej množinou hodnôt je interval .

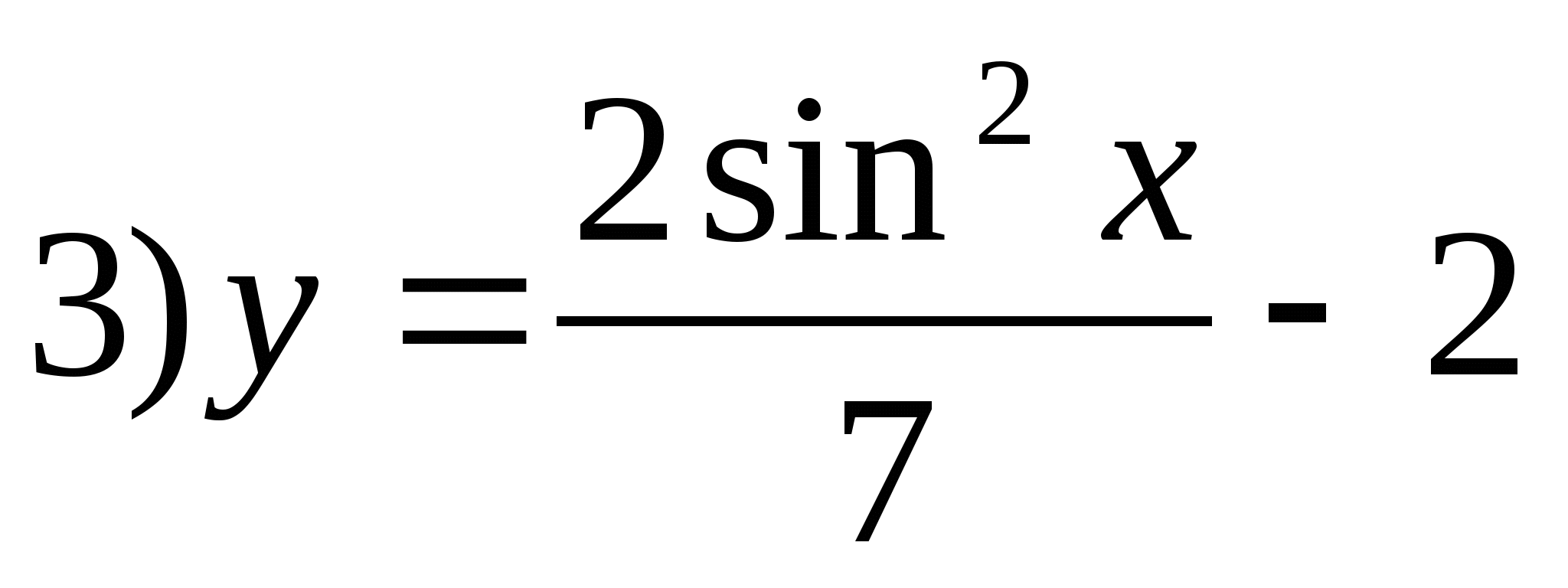


6. Zadajte najväčšie záporné celé číslo, ktoré nie je zahrnuté v rozsahu funkcie 
1) -1 2) -25 3) -6 4) -2
7. Koľko celých čísel patrí do množiny funkčných hodnôt 
1) 11 2) 3 3) 5 4) 4
Možnosť 5
1. Zadajte množinu funkčných hodnôt y = 2 -hriech 5 X.
1) (2;5) 2) 3) (1;3) 4) [-3;7]
2. Nájdite rozsah funkcie 
1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)
3. Zadajte najmenšie celé číslo z rozsahu funkcie
r = 3 + hriech 2 2 X.
1) 0 2) 1 3) 3 4) 4
4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt 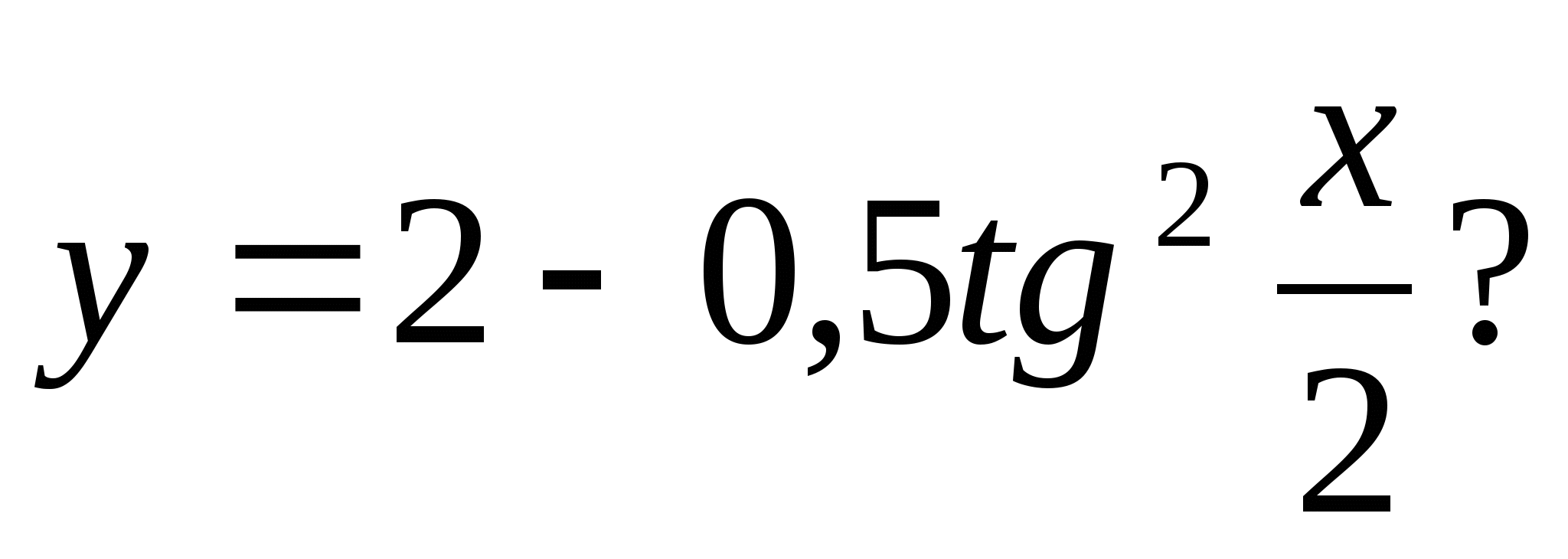
1) 128 2) 10,5 3) 3 4) -235
5. Zadajte funkciu, ktorej množinou hodnôt je segment [-9;15].

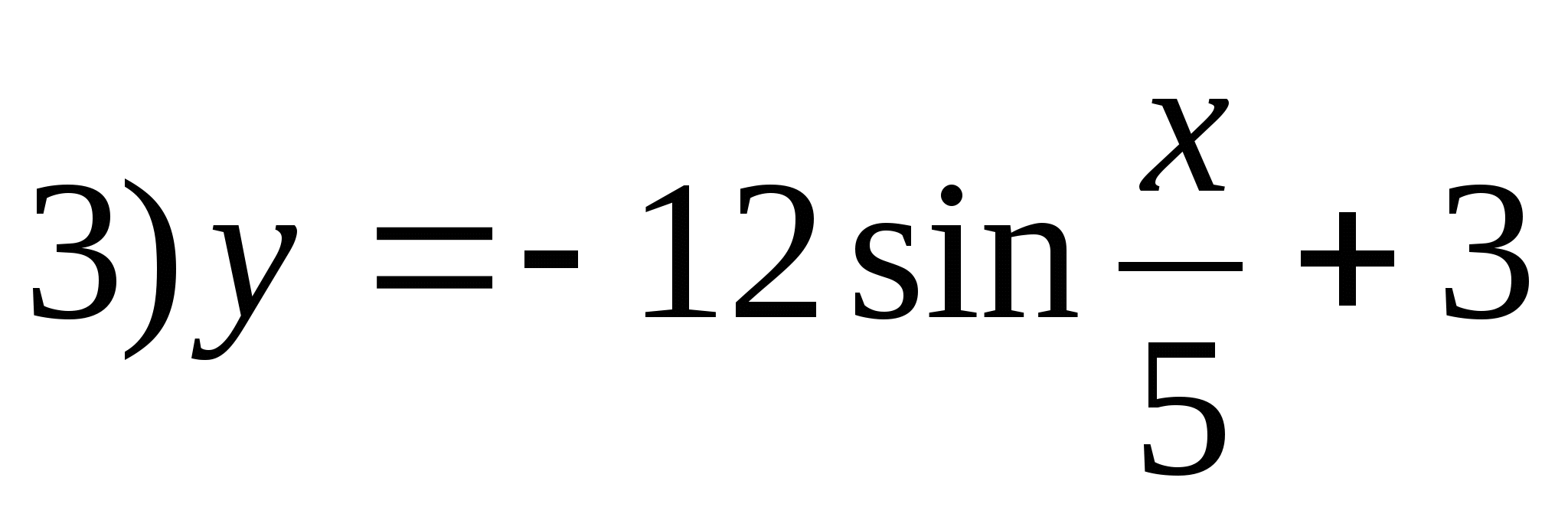


6. Nájdite súčet celých čísel zahrnutých v množine funkčných hodnôt 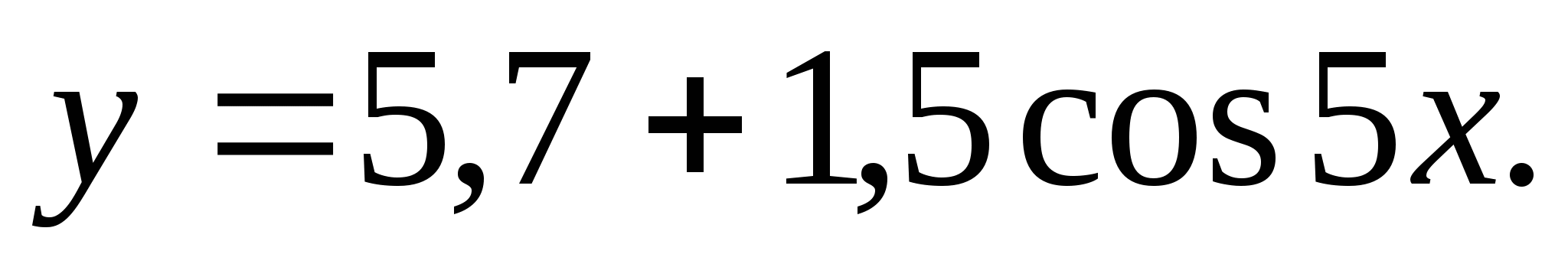
1) 0 2) 7 3) 18 4) 22
7. Nájdite najväčšiu hodnotu funkcie  na segmente
na segmente 
1) 0,5 2) 1,5 3) 0 4) 2
Možnosť 6
1. Zadajte segment zodpovedajúci množine funkčných hodnôt 
1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]
2. Nájdite rozsah funkcie 
3. Zadajte najväčšie číslo z rozsahu funkcie 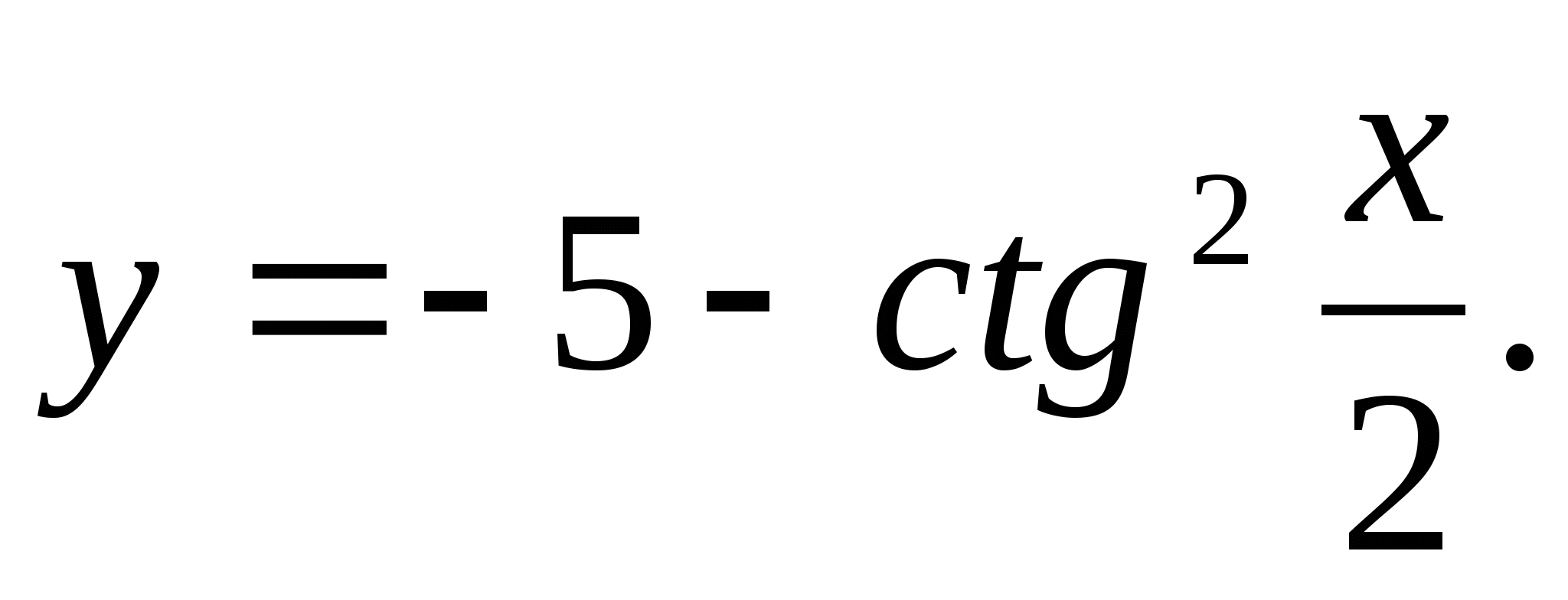
1) 5 2) -6 3) -3 4) 4
4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt 
1) 5 2) 0 3) -3 4) 4
5. Zadajte funkciu, ktorej množinou hodnôt je interval .
1) pri = 15 – 7 cos 2x 3) y = 7 cos 2x + 3
2) r = 5 cos 4 X 4) r = - tg 2 X + 1
6. Nájdite súčin celých čísel zahrnutých v množine hodnôt
r = 3,8 – 1,4 hriech 3 X.
1) 17 2) 12 3) 0 4) 60
7. Nájdite množinu funkčných hodnôt 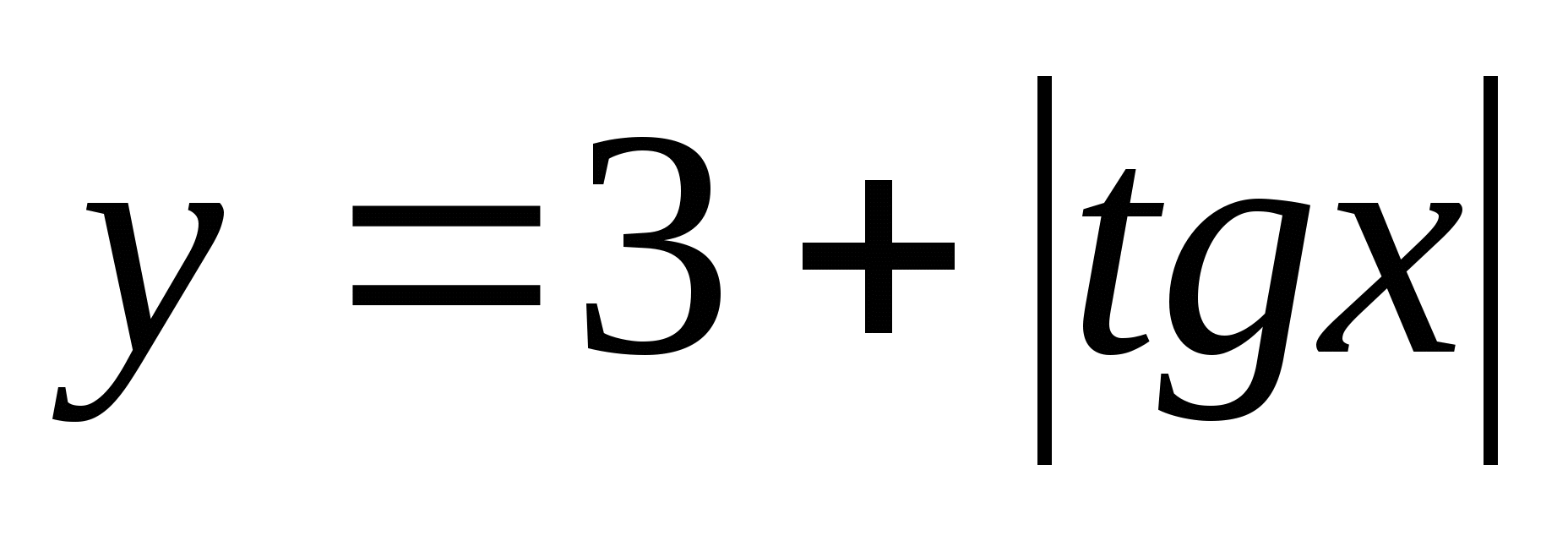 medzi
medzi 
1) (3;4) 2) 3)
Možnosť 7



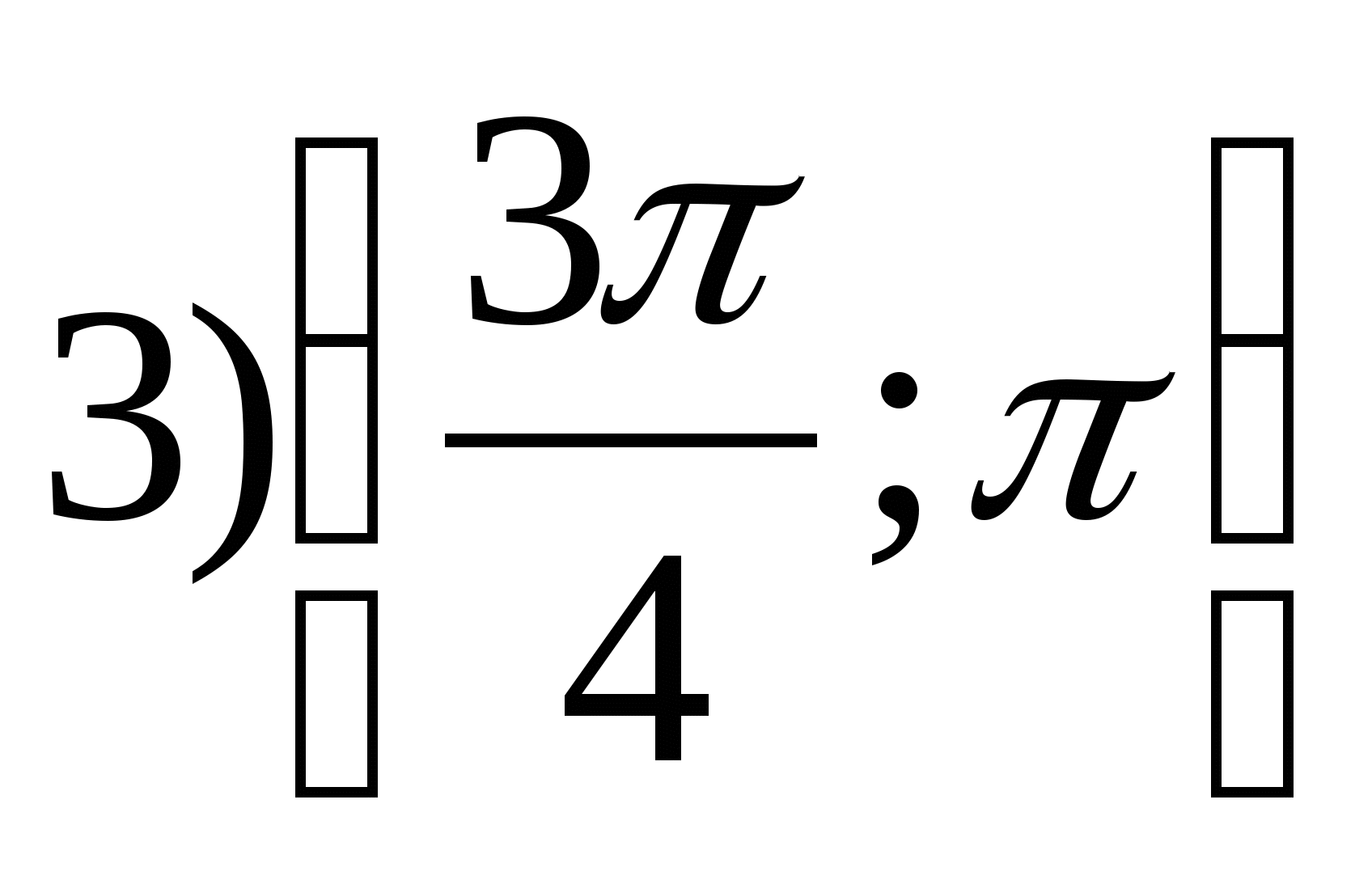

2. Nájdite najmenšiu celočíselnú hodnotu funkcie 
1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6
4. Pre aké hodnoty a platí rovnicahriech(3 X-4)+5= a riešiteľné?
1) 2) 3) (4;6) 4) (-6;4]
hriech 2 2 X – 2.
1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]
 medzi
medzi 
 2) 0 3) 1
2) 0 3) 1

r = 4 hriech(X 4 ) -2?
1) 8 2) 9 3) 7 4) 10
Možnosť 8
1. Nájdite množinu funkčných hodnôtr = arctgX- 2π.
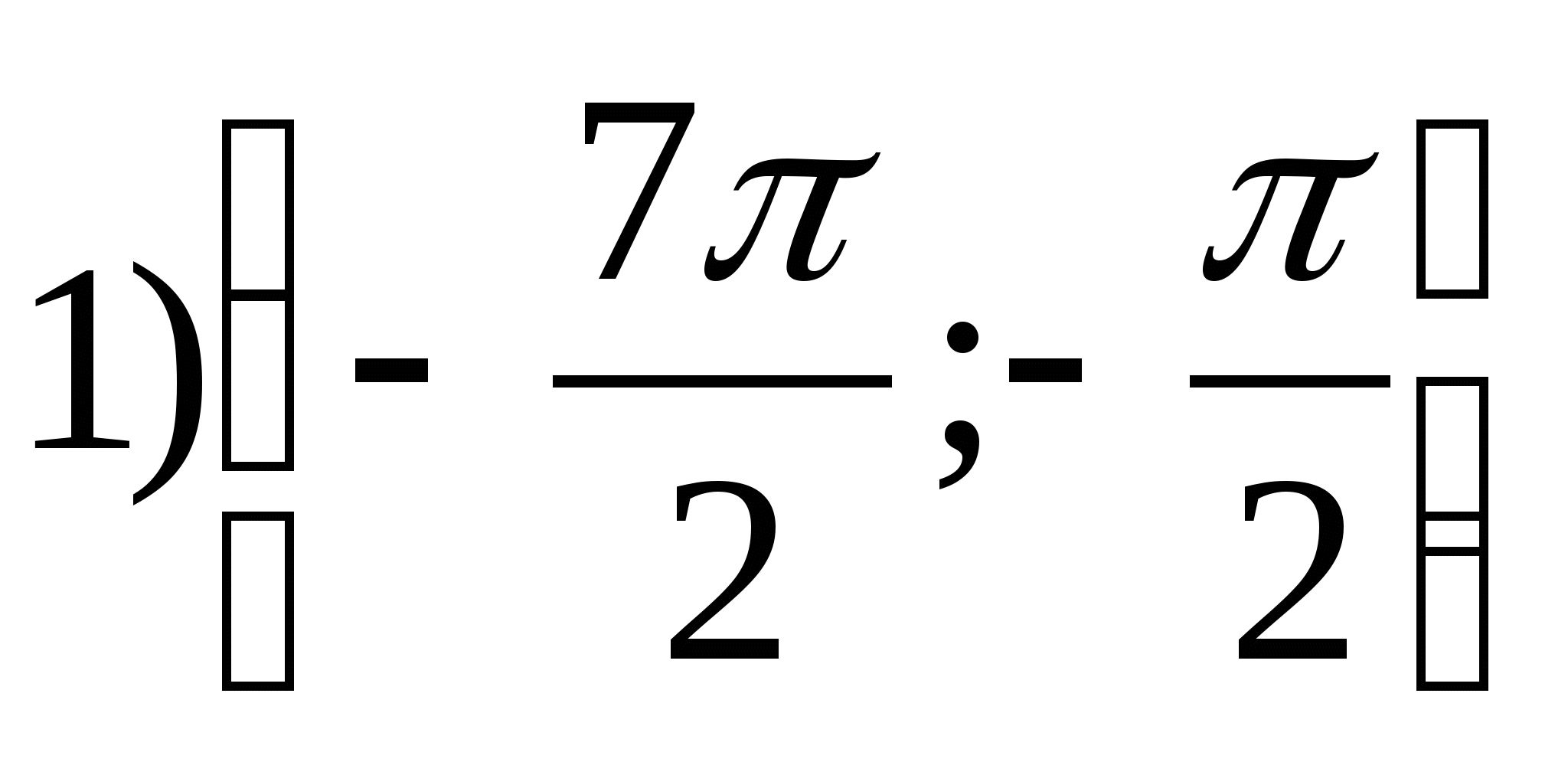
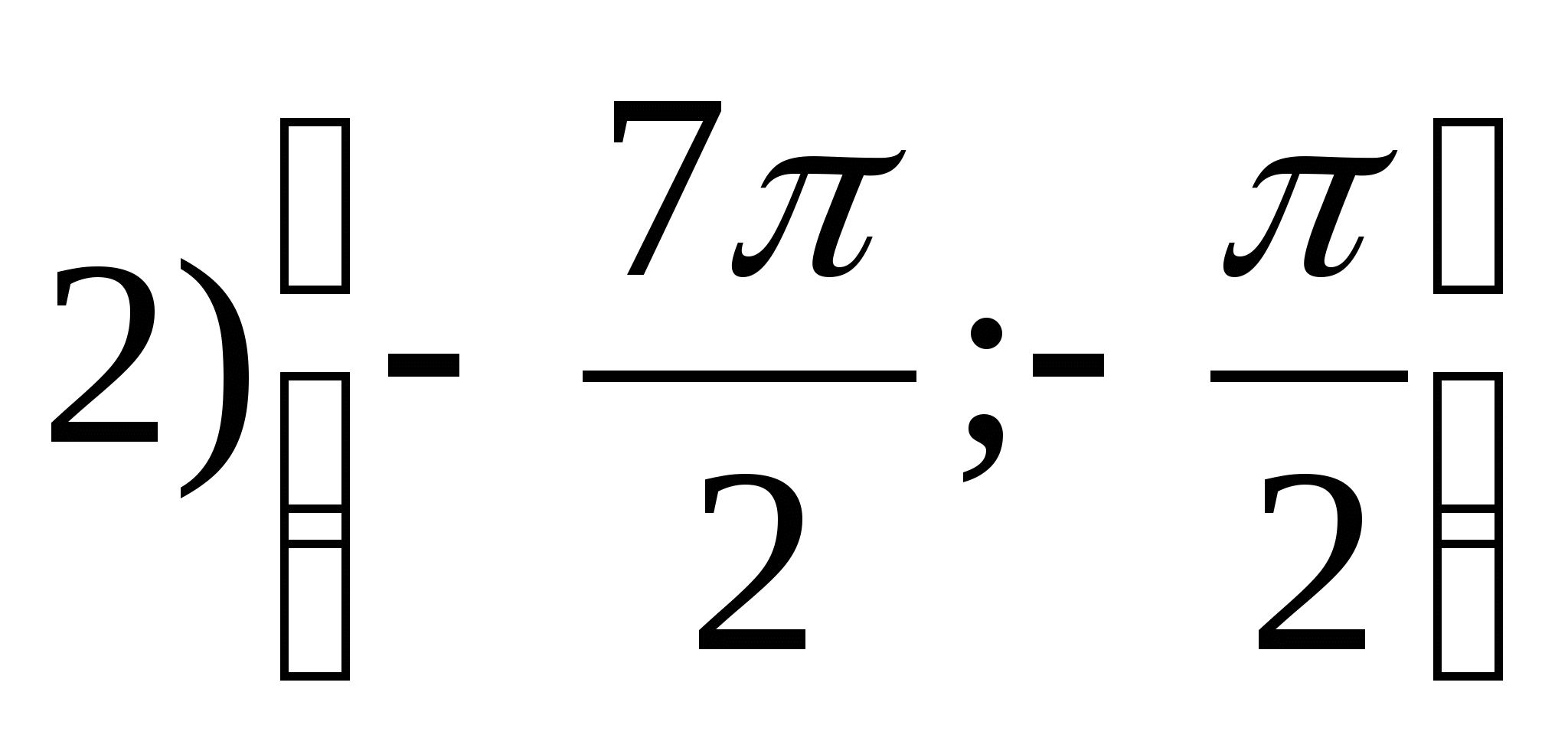

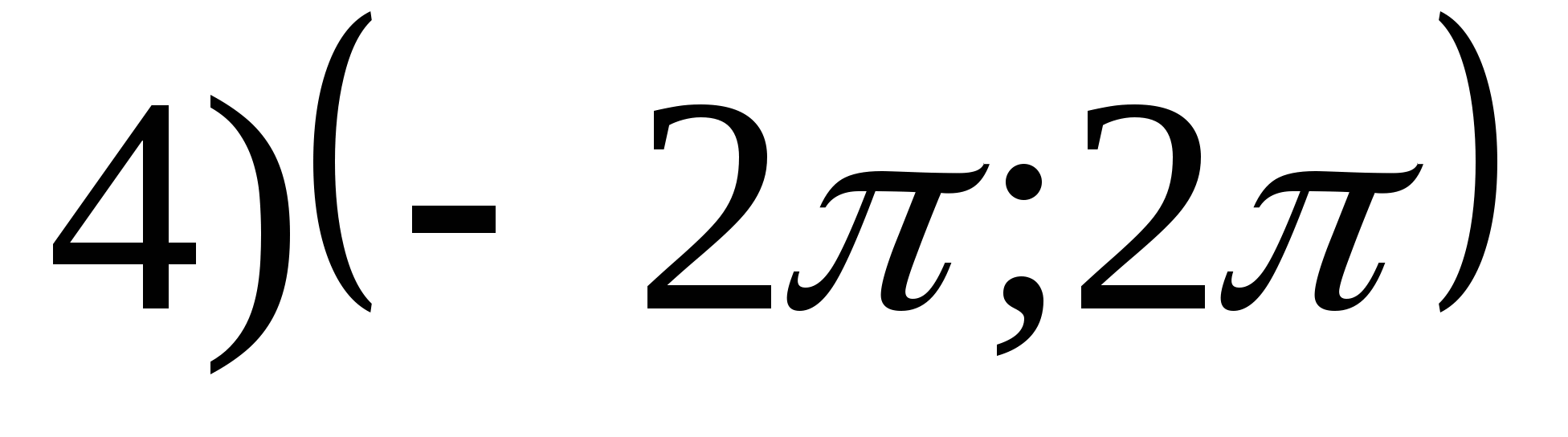
2. Nájdite najväčšiu hodnotu funkcie 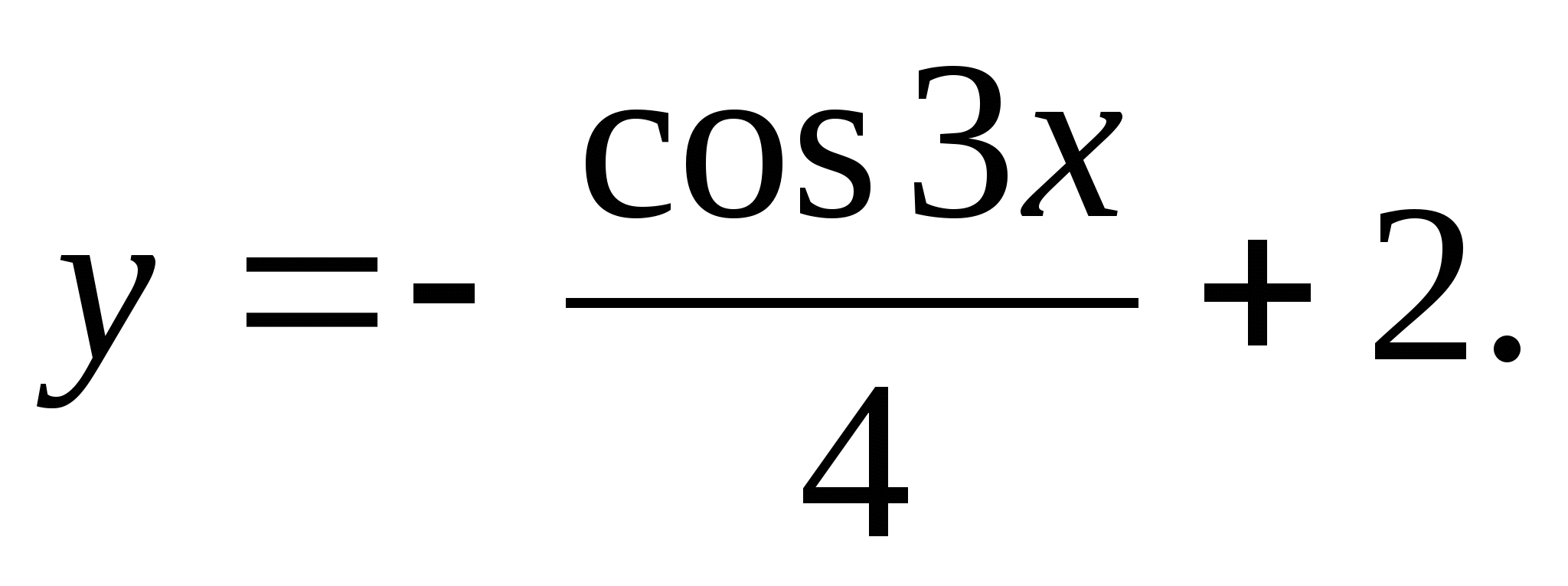
1) 1,75 2) 0 3) 2,25 4) -1,75
3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie 
1) -4 2) -2 3) 0 4) 2
4. Pre aké hodnoty p rovnice -2+cos(4 X-1)= p má korene?
1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)
5. Nájdite množinu funkčných hodnôtr = -2 tg 2 X + 1.
1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)
 medzi
medzi  .
.
1) 0 2) 1 3) -1 4) 3
7. Koľko celých čísel je v rozsahu funkcie
1) 4 2) 3 3) 5 4) 2
Možnosť 9
1. Nájdite rozsah funkcie 
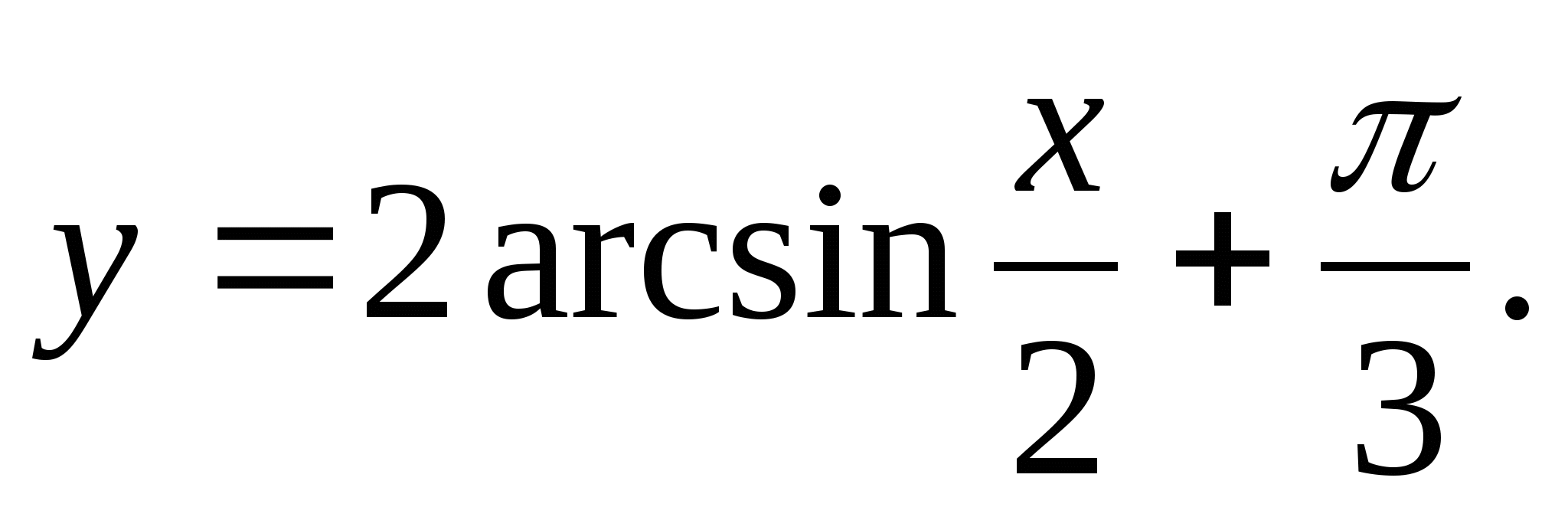

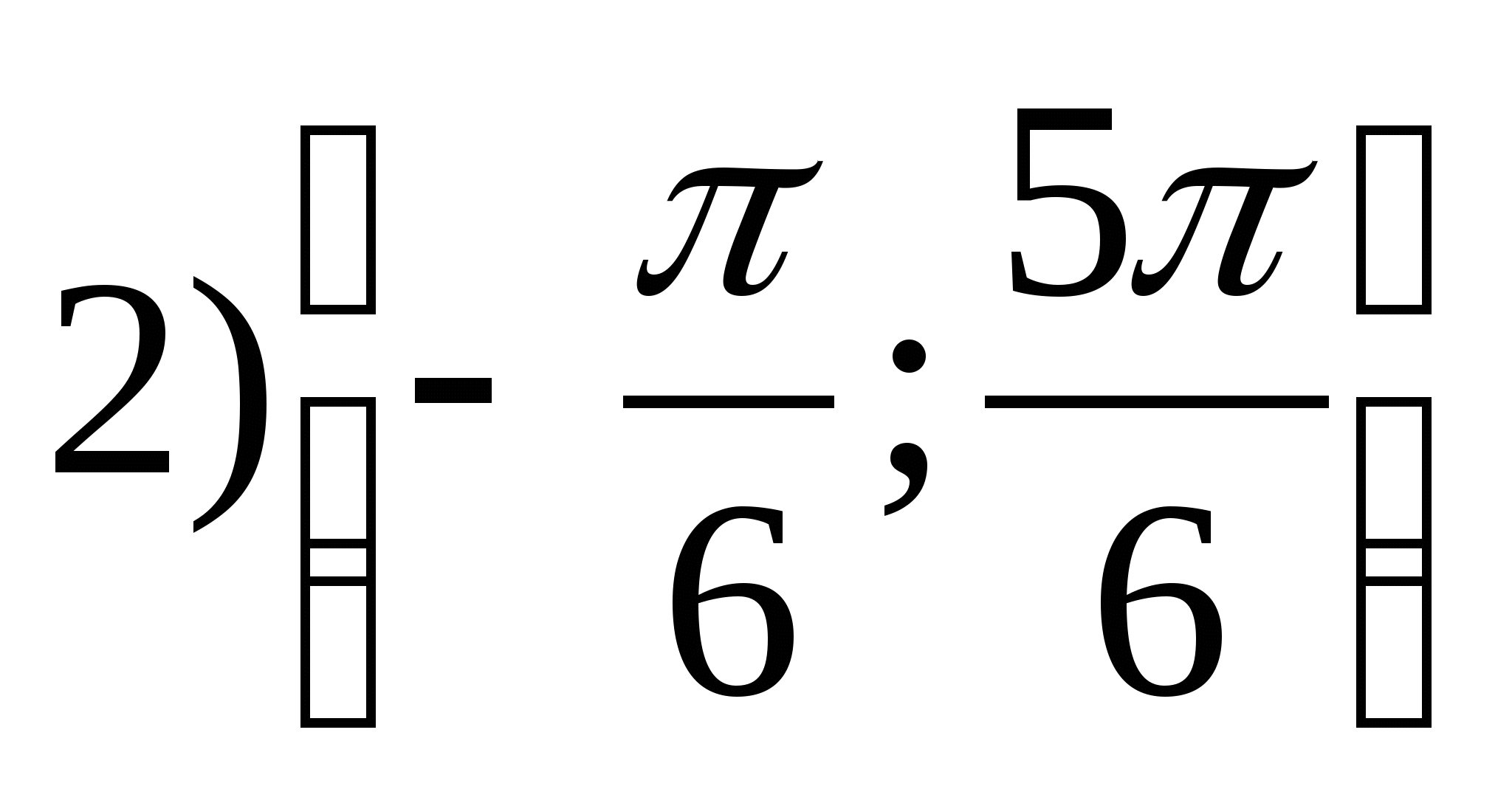


2. Nájdite najväčšiu celočíselnú hodnotu funkcie 
1) 4 2) 5 3) 6 4) 7
3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie 
1) 0 2) 3 3) 6 4) 9
k rovnica - k + hriech(2 X-1) = 2 riešiteľné?
1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]
5. Nájdite množinu funkčných hodnôt podľa \u003d -cos 2 3 X + 4.
1) 2) 3) 4)
6. Zadajte najmenšiu hodnotu funkcie  medzi
medzi 
 2) -1 3) 0 4) 1
2) -1 3) 0 4) 1
7. Zistite, koľko celých čísel je v rozsahu funkcie y = 12cos 3 X +5 hriech 3 X.
1) 13 2) 27 3) 26 4) 14
Možnosť 10
1. Nájdite rozsah funkcie 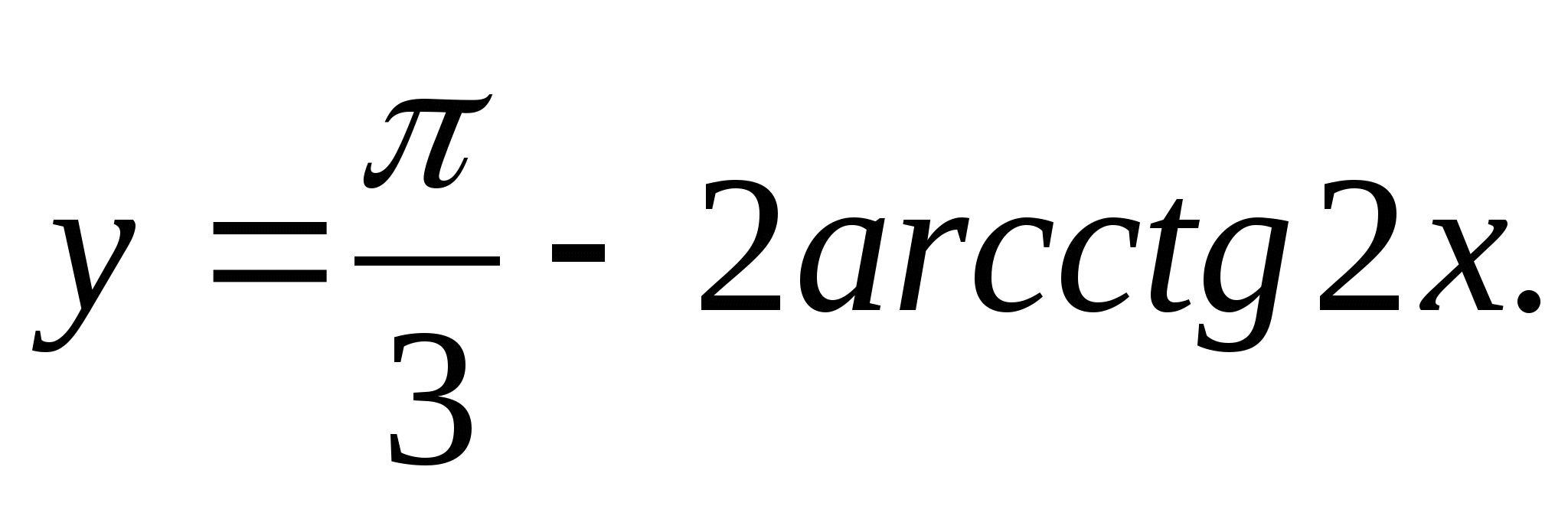


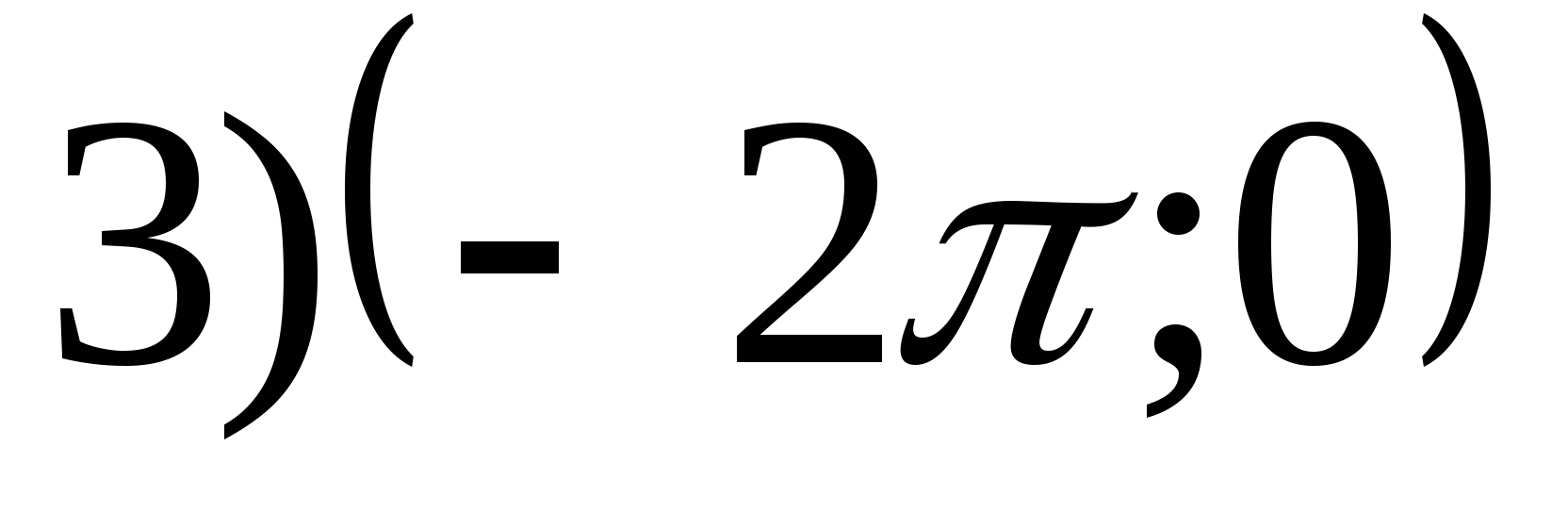
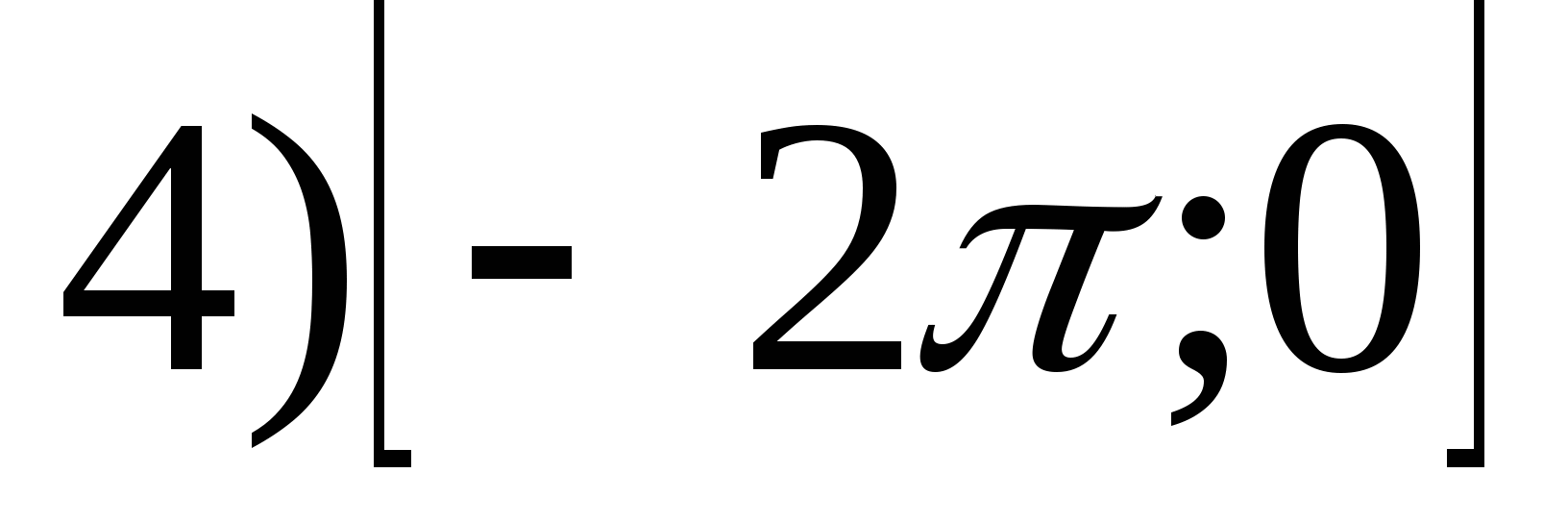
2. Nájdite najmenšiu hodnotu funkcie 
1) 3,5 2) 0 3) 2,5 4) -3,5
3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie 
1) -4 2) -1 3) 3 4) 7
4. Pri akých hodnotách parametram rovnica cos (3 X + 2)- m= 5 má korene?
1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]
5. Nájdite množinu funkčných hodnôt podľa \u003d -2ctg 2 3 X + 7.
1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]
6. Zadajte najväčšiu hodnotu funkcie  medzi
medzi 
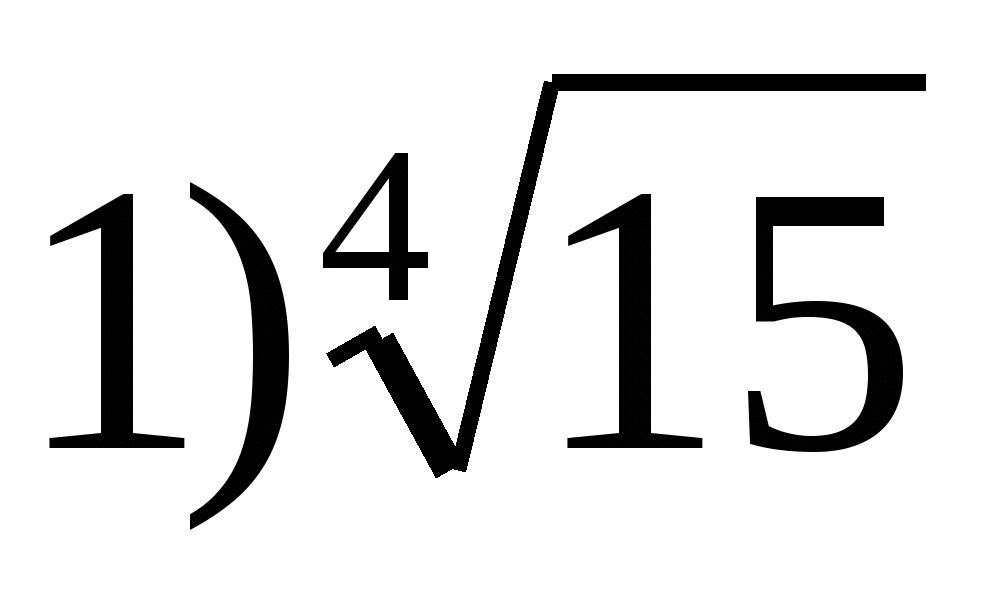 2) 0 3) 2 4) 1
2) 0 3) 2 4) 1
7. Zistite, koľko celých čísel je v rozsahu funkcie 
1) 30 2) 35 3) 17 4) 7
Sada hodnôt exponenciálnych a logaritmických funkcií
možnosť 1
1. Nájdite rozsah funkcie 
1) 4) (-∞;3)
2. Zadajte množinu funkčných hodnôt 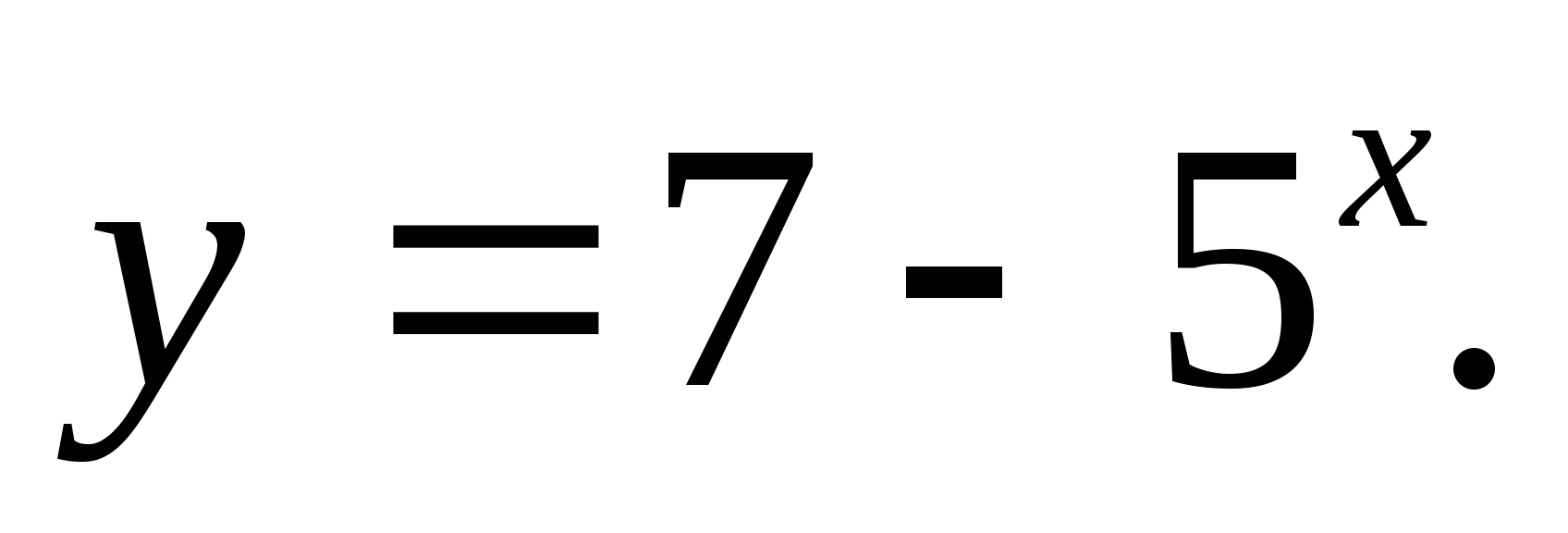
1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)
6. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) 1 2) -1 3) 0 4) -5
7. Zadajte funkciu, ktorej množinou hodnôt je interval (1;∞).
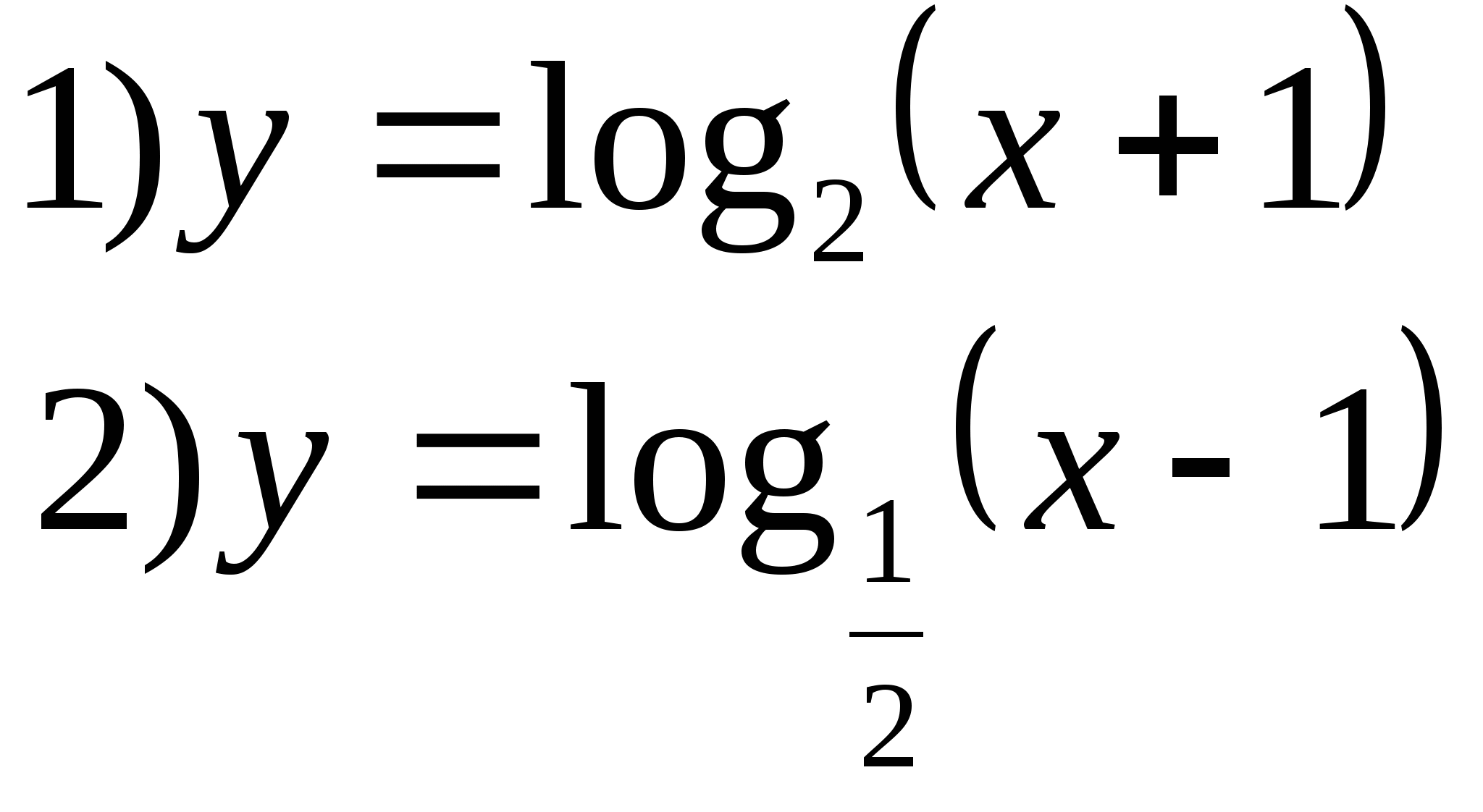

Možnosť 2
1. Zadajte množinu funkčných hodnôt 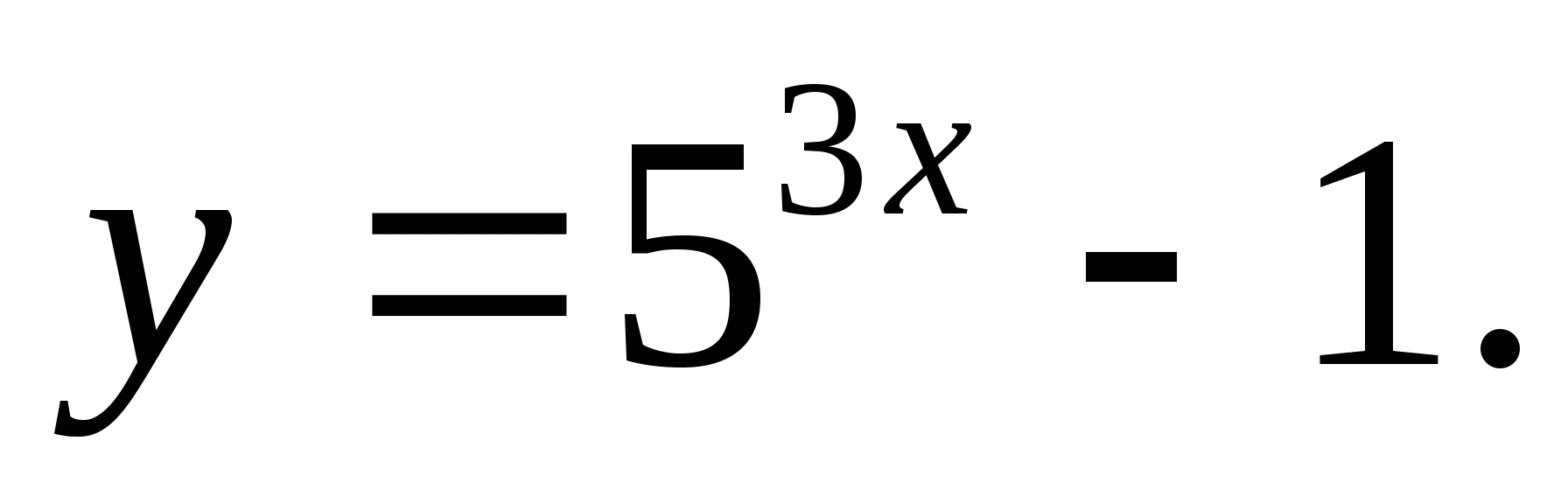
1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)
2. Nájdite rozsah funkcie 
1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)
3. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) -12 2) -11 3) -10 4) -15
4. Zadajte číslo, ktoré nepatrí do množiny funkčných hodnôt 
1) -42 2) 3 3) 1 4) -20
5. Zadajte množinu funkčných hodnôt 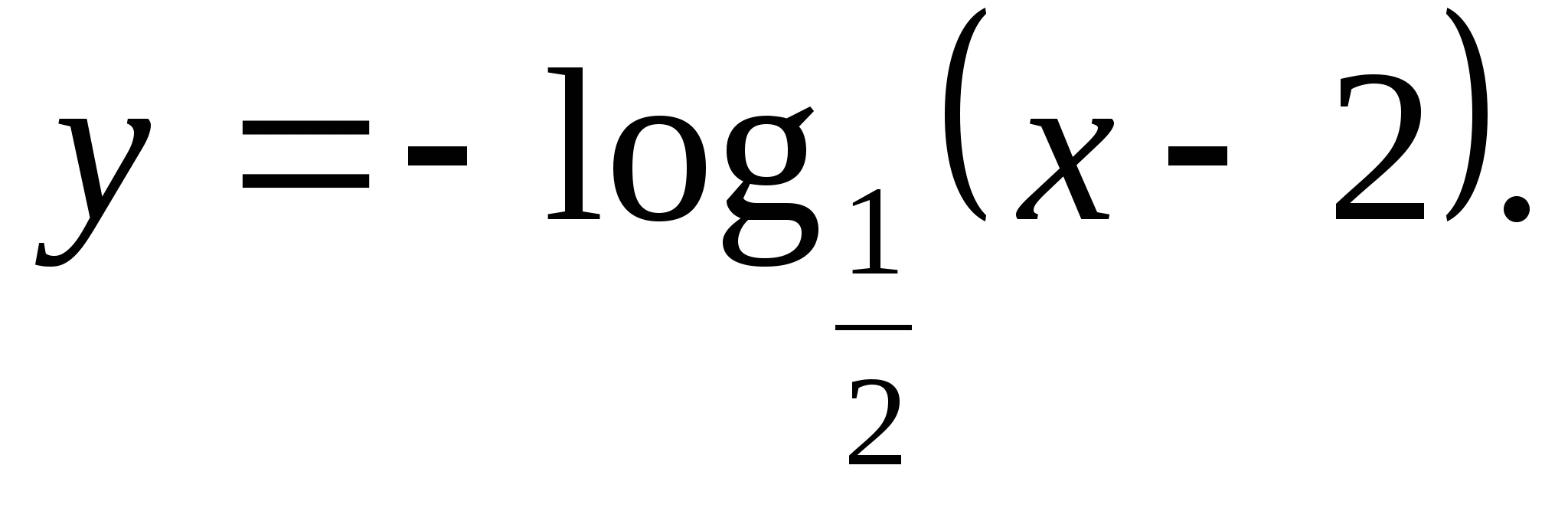
1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]
6. Zadajte najväčšiu celočíselnú hodnotu funkcie 
1) 10 2) 3 3) 9 4) 2
7. Zadajte funkciu, ktorej množinou hodnôt je interval
(-∞;13).


Možnosť 5
1. Zadajte najmenšiu celočíselnú hodnotu funkcie 
1) 0 2) -1 3) -2 4) -3
2. Ktoré z nasledujúcich čísel je v rozsahu funkcie 
1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)
6. Nájdite, na ktorom segmente je funkcia  nadobúda najväčšiu hodnotu 2 a najmenšiu hodnotu -3.
nadobúda najväčšiu hodnotu 2 a najmenšiu hodnotu -3.
1) 2) (-5;2) 3) 4) (-3;2)
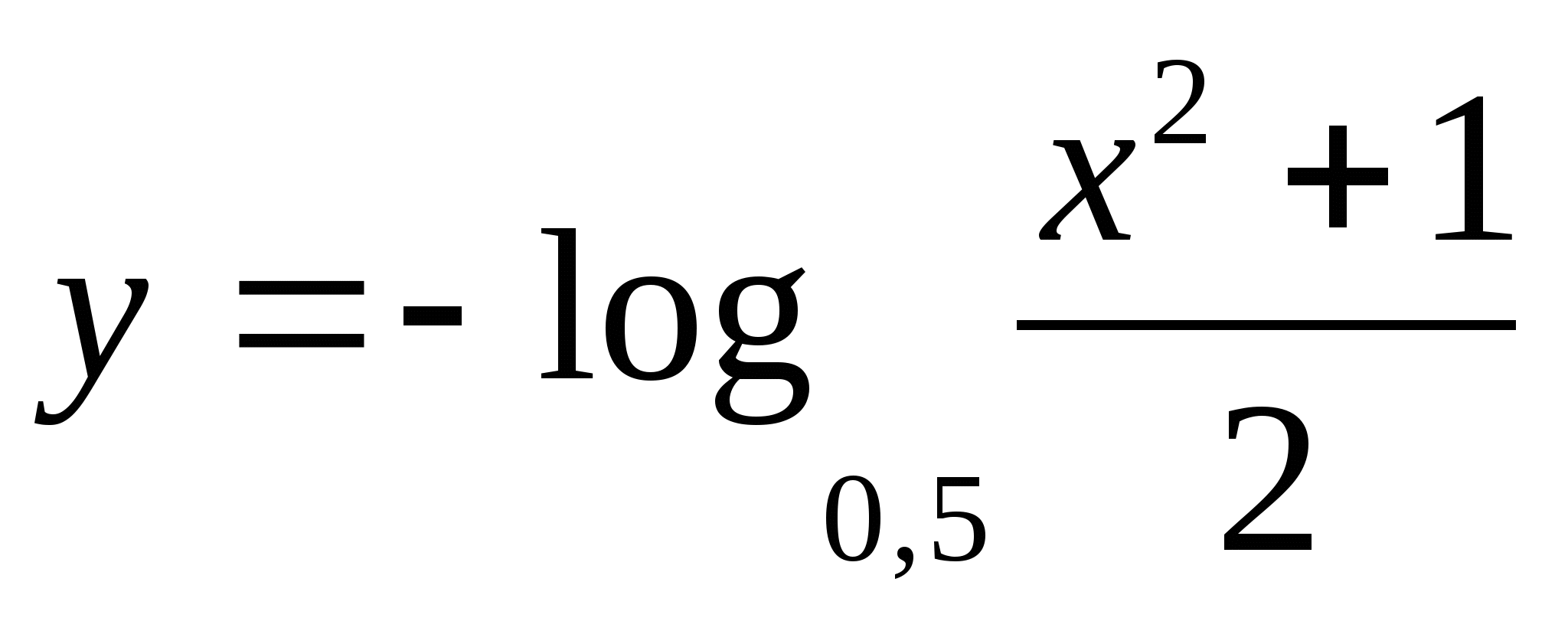 medzi
medzi 
1) -1/2 2) 5 3) 2 4) 4
8. Nájdite súčet všetkých prirodzených čísel, ktoré nie sú zahrnuté v množinách hodnôt funkcie 
1) 3 2) 6 3) 10 4) 8
Možnosť 6
1. Zadajte najväčšiu celočíselnú hodnotu funkcie 
1) 2 2) 4 3) 3 4) 5
2. Ktoré z nasledujúcich čísel nie je v rozsahu funkcie 
1) 35 2) 7, 28 3) 7, 85 4) 128
3. Zadajte množinu funkčných hodnôt 
1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)
4. Nájdite všetky body na OU, ktoré sú projekciami bodov grafu funkcie 
1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)
6. Nájdite, na ktorom segmente je funkcia 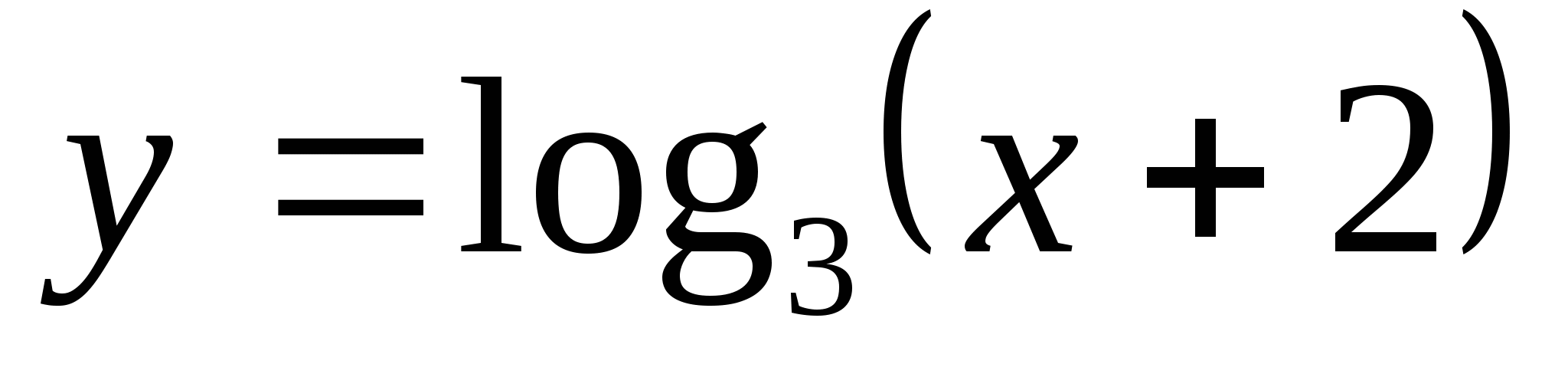 má najmenšiu hodnotu ako -2 a najväčšiu hodnotu ako 4.
má najmenšiu hodnotu ako -2 a najväčšiu hodnotu ako 4.
1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)
7. Zadajte najväčšiu hodnotu funkcie  medzi
medzi
[-0,9; 0]. 2. Nájdite najmenšiu hodnotu funkcie na segmente.
4. Koľko celočíselných hodnôt má funkcia 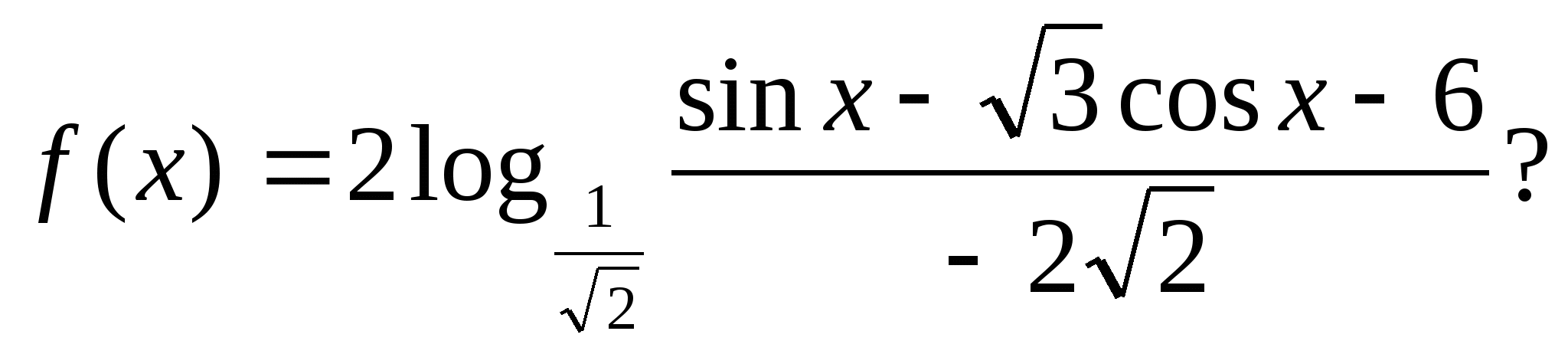
Odpovede
Časť 1
Množina hodnôt exponenciálnych a logaritmických funkcií
Časť 2
Funkciou je model. Definujme X ako množinu hodnôt nezávislej premennej // nezávislý znamená ľubovoľný.
Funkcia je pravidlo, podľa ktorého pre každú hodnotu nezávislej premennej z množiny X možno nájsť jedinú hodnotu závisle premennej. // t.j. pre každé x je jedno y.
Z definície vyplýva, že existujú dva pojmy - nezávislá premenná (ktorú označíme x a môže nadobudnúť ľubovoľnú hodnotu) a závislá premenná (ktorú označíme y alebo f (x) a vypočíta sa z funkcie, keď nahrádzame x).
NAPRÍKLAD y=5+x
1. Nezávislé je x, takže vezmeme ľubovoľnú hodnotu, nech x = 3
2. a teraz vypočítame y, takže y \u003d 5 + x \u003d 5 + 3 \u003d 8. (y je závislé od x, pretože to, čo x dosadíme, dostaneme také y)
Hovoríme, že premenná y je funkčne závislá od premennej x a označíme ju takto: y = f (x).
NAPRÍKLAD.
1,y = 1/x. (nazývané hyperbola)
2. y=x^2. (nazýva sa parabola)
3.y=3x+7. (nazývaná priama čiara)
4. y \u003d √ x. (nazýva sa vetva paraboly)
Nezávislá premenná (ktorú označujeme x) sa nazýva argument funkcie.
Množina všetkých hodnôt, ktoré má argument funkcie, sa nazýva doména funkcie a označuje sa D(f) alebo D(y).
Uvažujme D(y) pre 1.,2.,3.,4.
1. D (y)= (∞; 0) a (0;+∞) //celá množina reálnych čísel okrem nuly.
2. D (y) \u003d (∞; +∞) / / všetkých veľa reálnych čísel
3. D (y) \u003d (∞; +∞) / / všetkých veľa reálnych čísel
4. D (y) \u003d)