Lahodné čokoládové palacinky za pol hodiny
Zdravé jedlo by malo byť chutné, aby vyvolalo chuť do jedla, pretože jeho účelom nie je len dodať telu cenné...
Simplexná metóda je metóda postupného prechodu z jedného základného riešenia (vrchol mnohostenu riešení) sústavy obmedzení úlohy lineárneho programovania k inému základnému riešeniu, kým cieľová funkcia nenadobudne optimálnu hodnotu (maximum alebo minimum).
Simplexová metóda je univerzálna metóda, ktorá dokáže vyriešiť akúkoľvek problém lineárneho programovania, pričom grafická metóda je vhodná len pre systém obmedzení s dvoma premennými.
Simplexovú metódu navrhol americký matematik R. Danzig v roku 1947, odvtedy sa táto metóda pre potreby priemyslu často používa na riešenie problémov lineárneho programovania s tisíckami premenných a obmedzení.
Predtým, ako prejdeme k algoritmu simplexnej metódy, niekoľko definícií.
Akékoľvek nezáporné riešenie systému obmedzení sa nazýva prijateľné rozhodnutie .
Nech existuje systém m obmedzenia s n premenné ( m n).
Prijateľné základné riešenie je roztok obsahujúci m nezáporné hlavný (základné ) premenné a n - m nejadrový ... (nezákladné, príp zadarmo ) premenné. Vedľajšie premenné v základnom riešení sú rovné nule, zatiaľ čo hlavné premenné sú spravidla nenulové, to znamená, že sú to kladné čísla.
akýkoľvek m systémové premenné m lineárne rovnice s n premenné sa nazývajú hlavný ak je determinant koeficientov pri nich nenulový. Potom zvyšok n - m premenné sa nazývajú nemainstreamové (alebo zadarmo ).
Dôležité podmienky
Niektoré špeciálne prípady sú popísané v samostatných článkoch: kedy maximum účelovej funkcie je nekonečno, kedy systém nemá riešenie, a kedy optimálne riešenie nie je jediné .
Ďalej analyzujme typický príklad, keď je systém obmedzení spojený a existuje konečné optimum, jediné. Variáciou simplexovej metódy je distribučný spôsob riešenia dopravného problému .
Je oveľa jednoduchšie vyriešiť problém lineárneho programovania konštrukciou simplexných tabuliek ako použitím algebraických transformácií, čo je znázornené v ďalšej časti. Simplexné tabuľky sú veľmi popisné. Existuje niekoľko typov pravidiel pre prácu s simplexnými tabuľkami. Pozrime sa na to, čo sa najčastejšie nazýva pravidlo úvodného stĺpca a úvodného riadka.
Nebude zbytočné otvárať príručku Akcie so zlomkami v novom okne: je ich dosť, zlomkov v úlohách na simplexnej metóde, mierne povedané.
Príklad.
Zavádzame ďalšie nezáporné premenné a redukujeme tento systém nerovností na ekvivalentný systém rovníc

![]() .
.
Stalo sa to v súlade s nasledujúcim pravidlom: ak je v pôvodnom obmedzení znamienko „menšie alebo rovné“, musí sa pridať dodatočná premenná a ak „väčšie alebo rovné“, musí sa dodatočná premenná odpočítať.
Zavedené dodatočné premenné sa berú ako hlavné (základné). Potom a sú nezákladné (voľné) premenné.
Vyjadrením hlavných (základných) premenných z hľadiska nezákladných (voľných) premenných dostaneme

Cieľovú funkciu môžeme vyjadriť aj pomocou nezákladných (voľných) premenných:
![]()
Z koeficientov premenných (neznámych) zostrojíme prvú simplexnú tabuľku.
| stôl 1 | ||||
| Základné neznáme | Voľní členovia | Voľné neznáme | Pomocné koeficienty | |
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Posledný riadok tabuľky, ktorý obsahuje cieľovú funkciu a koeficienty voľných premenných v nej, sa bude nazývať indexový riadok.
Získané riešenie nie je optimálne, keďže koeficienty voľných premenných v indexovom riadku sú záporné. To znamená, že optimálne riešenie bude také, v ktorom sú koeficienty voľných premenných v indexovej línii väčšie alebo rovné nule.
Ak chcete prejsť na ďalšiu tabuľku, nájdeme najväčšie (modulo) z čísel a. Toto je číslo 2. Vedúci stĺpec je teda stĺpec, v ktorom je napísané
Na určenie vedúceho riadku nájdeme minimum pomeru voľných členov k prvkom vedúceho stĺpca, a ak má čitateľ kladné číslo a menovateľ je záporný, pomer sa považuje za rovný nekonečnu.
![]() .
.
Preto je vedúcou líniou tá, v ktorej je napísaná
Vedúci prvok je teda -2.
Vytvorte druhú simplexnú tabuľku.
Do prvého riadku zadáme nový základný prvok a do stĺpca, v ktorom stál, zadáme novú voľnú premennú
Vyplníme prvý riadok. Za týmto účelom vydelíme všetky čísla v poprednom riadku tabuľky 1 pivotom a zapíšeme ich do zodpovedajúceho stĺpca prvého riadku tabuľky 2, okrem čísla v poprednom stĺpci, kde je inverzná hodnota pivota sa píše (teda jednotka delená vedúcim prvkom).
Vyplníme stĺpec pomocných koeficientov. Pre toto číslo vedúceho stĺpca tabuľky 1 zapíšeme do stĺpca pomocných koeficientov tabuľky 2 okrem vedúceho prvku aj opačnými znamienkami.
| tabuľka 2 | ||||
| Základné neznáme | Voľní členovia | Voľné neznáme | Pomocné koeficienty | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Tí, ktorí si ešte neotvorili príručku Operácie so zlomkami v novom okne, môžu tak urobiť teraz, pretože je správny čas.
Na získanie zostávajúcich riadkov tabuľky 2 sa čísla už v prvom riadku tejto tabuľky vynásobia pomocným koeficientom v riadku, ktorý sa má vyplniť, a k výsledku pripočítame číslo z tabuľky 1 v tom istom riadku so zodpovedajúcim premenlivý.
Napríklad, aby sme získali voľný termín druhého riadku, vynásobíme číslo 1 číslom 1 a pridáme číslo -4 z tabuľky 1. Dostávame -3. Koeficient at v druhom riadku nájdeme rovnakým spôsobom: ![]() ... Keďže predchádzajúca tabuľka nemá stĺpec s novou voľnou premennou, koeficient druhého riadku v stĺpci novej voľnej premennej bude
... Keďže predchádzajúca tabuľka nemá stĺpec s novou voľnou premennou, koeficient druhého riadku v stĺpci novej voľnej premennej bude ![]() (teda z tabuľky 1 pripočítame 0, keďže v tabuľke 1 nie je stĺpec c).
(teda z tabuľky 1 pripočítame 0, keďže v tabuľke 1 nie je stĺpec c).
Indexový riadok je tiež vyplnený:

Takto získané riešenie opäť nie je optimálne, keďže v indexovom riadku sú koeficienty voľných premenných opäť záporné.
Aby sme prešli na ďalšiu simplexnú tabuľku, nájdeme najväčšie (modulo) z čísel a to znamená moduly koeficientov v riadku indexu. Toto je číslo 2. Vedúci stĺpec je teda stĺpec, v ktorom je napísané.
Pre hľadanie vedúceho radu nájdeme minimum vzťahu voľných členov k prvkom vedúceho radu. Dostaneme:
![]() .
.
Preto je vodiaca čiara tá, v ktorej je napísaná, a vodiaci prvok je -3/2.
Vytvorenie tretieho simplexného stola
V prvom riadku sa zapíše nová základná premenná. Do stĺpca, v ktorom bola, zadáme novú voľnú premennú.
Prvá línia:

Pomocné koeficienty:
![]()
| Tabuľka 3 | ||||
| Základné neznáme | Voľní členovia | Voľné neznáme | Pomocné koeficienty | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | -1/2 |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |

Získané riešenie opäť nie je optimálne, keďže koeficienty voľných neznámych v indexovom riadku sú opäť záporné.
Ak chcete prejsť na štvrtú simplexnú tabuľku, nájdeme najväčšie z čísel a. Toto je číslo.
Vedúci stĺpec je teda ten, v ktorom je napísaný.
Minimálne moduly vzťahov voľných členov k prvkom vedúceho stĺpca:
![]() .
.
Preto je vodiaca čiara tá, v ktorej je napísaná, a vodiaci prvok je 1/3.
Do štvrtej simplexnej tabuľky napíšte novú základnú premennú do prvého riadku. Do stĺpca, kde to bolo, napíšeme novú voľnú premennú.
Prvá línia:
Pomocné koeficienty:
| Tabuľka 4 | ||||
| Základné neznáme | Voľní členovia | Voľné neznáme | Pomocné koeficienty | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Výpočet zostávajúcich riadkov pomocou príkladu druhého riadku:

Získané riešenie tiež nie je optimálne, ale je už lepšie ako predchádzajúce, pretože jeden z koeficientov voľných premenných v riadku indexu je nezáporný.
Aby sme plán zlepšili, prejdime k ďalšej simplexnej tabuľke.
Nájdeme najväčšie z čísel 4 a. Toto je číslo 4. Preto vedúci stĺpec.
Ak chcete nájsť vedúcu čiaru, nájdite
![]() .
.
Preto je vedúcou líniou tá, v ktorej je napísaná. Ale už boli spolu medzi voľnými premennými. Preto, aby sme preniesli ďalšiu premennú z voľnej do základnej, zvolíme iný vedúci stĺpec - ten, v ktorom je zapísaná.
Ak chcete nájsť vedúcu čiaru, nájdite
![]() .
.
Preto je kľúčový riadok ten, v ktorom je napísaný, a vedúci prvok je 1.
V piatej simplexnej tabuľke zapíšeme novú základnú premennú do prvého riadku. Do stĺpca, kde to bolo, napíšeme novú voľnú premennú.
Prvá línia:
Pomocné koeficienty:
| Tabuľka 5 | ||||
| Základné neznáme | Voľní členovia | Voľné neznáme | Pomocné koeficienty | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Skúsme hneď zistiť, či riešenie nie je optimálne. Preto pre zvyšok riadkov počítame iba voľné členy (aby sme zistili hodnoty základných premenných, keď sa voľné premenné rovnajú nule) a koeficienty voľných premenných v riadku indexu.
Voľní členovia:
V druhom riadku;
Na treťom riadku;
Na štvrtom riadku.
Indexový reťazec:
Pozrime sa na simplexnú tabuľku 5. Vidíme, že sme získali optimálne riešenie, keďže koeficienty voľných neznámych v riadku indexu sú nezáporné.


Vyriešme algebraickými transformáciami rovnaký príklad ako v predchádzajúcej časti. Treba poznamenať, že pri riešení tohto druhu simplexovej metódy je lepšie nezapisovať cieľovú funkciu do formulára ![]() , pretože je ľahké sa zmiasť v znameniach. Ale v tomto prípade bude bod algoritmu definujúci kritérium optimality upravený nasledovne.
, pretože je ľahké sa zmiasť v znameniach. Ale v tomto prípade bude bod algoritmu definujúci kritérium optimality upravený nasledovne.
Ak sa hľadá maximum (minimum) lineárnej formy a v jej vyjadrení nie sú vedľajšie premenné s kladnými (zápornými) koeficientmi, potom je kritérium optimality splnené a získané základné riešenie je optimálne - riešenie je ukončené. Ak pri zistení maxima (minima) lineárnej formy jej vyjadrenie obsahuje jednu alebo viac vedľajších premenných s kladnými (zápornými) koeficientmi, prejdite na nové základné riešenie.
Príklad. Nájdite maximum funkcie v rámci obmedzení
Krok I. Zaveďte ďalšie nezáporné premenné a zredukujte tento systém nerovností na ekvivalentný systém rovníc

![]() .
.
Zavedené dodatočné premenné sa berú ako hlavné, keďže v tomto prípade možno ľahko nájsť základné riešenie systému. Potom a sú menšie premenné.
Vyjadrením hlavných premenných z hľadiska nehlavných dostaneme

Dané rozdelenie premenných na základné a nebázické teda zodpovedá základnému riešeniu ![]() čo je neplatné (dve premenné sú záporné), a preto nie je optimálne. Prejdime od tohto základného riešenia k vylepšenému.
čo je neplatné (dve premenné sú záporné), a preto nie je optimálne. Prejdime od tohto základného riešenia k vylepšenému.
Ak chcete rozhodnúť, ktorá premenná by sa mala preniesť z nezákladnej do základnej, zvážte ktorúkoľvek z dvoch existujúcich rovníc posledného systému so zápornými voľnými členmi, napríklad druhú. Ukazuje, že je možné prekladať a do hlavných premenných, keďže v tejto rovnici majú kladné koeficienty (preto s ich nárastom, a to sa stane, ak niektorú z nich prevedieme na hlavné premenné, premenná sa zvýši).
Skúsme to preložiť do hlavnej premennej. Aby sme určili, ktorá premenná sa má preniesť zo základnej do nebázickej, nájdeme absolútnu hodnotu najmenšieho pomeru voľných členov systému ku koeficientom at. Máme. Získava sa z tretej rovnice, ktorá ukazuje, že premennú, ktorá je v pôvodnom základnom riešení kladnú, je potrebné previesť na nebázické. V dôsledku toho získané zásadité riešenie, rovnako ako pôvodné, obsahuje dve negatívne zložky, t.j. pri prechode na takéto zásadité riešenie nedôjde k zlepšeniu.
Príklad 5.1. Vyriešte nasledujúci problém lineárneho programovania pomocou simplexnej metódy:
Riešenie:
ja iterácia:

x3, x4, x5, x6 x1,x2... Vyjadrime základné premenné z hľadiska voľných:

Preveďme účelovú funkciu do nasledujúceho tvaru:
Na základe získaného problému vytvoríme počiatočnú simplexnú tabuľku:
Tabuľka 5.3
Zdrojová simplexná tabuľka
Hodnotiace vzťahy |
||||
Podľa definície základného riešenia sa voľné premenné rovnajú nule a hodnoty základných premenných sa rovnajú zodpovedajúcim hodnotám voľných čísel, t.j.:
3. fáza: kontrola zlučiteľnosti systému obmedzenia LPP.
Pri tejto iterácii (v tabuľke 5.3) nebol identifikovaný znak nekompatibility systému obmedzení (znak 1) (tj neexistuje riadok so záporným voľným číslom (okrem riadku účelovej funkcie), čo by neobsahujú aspoň jeden záporný prvok (tj záporný koeficient pri voľnej premennej)).
Pri tejto iterácii (v tabuľke 5.3) nebolo identifikované znamienko neohraničenosti účelovej funkcie (znamienko 2) (tj v riadku účelovej funkcie nie je stĺpec so záporným prvkom (okrem stĺpca voľnej funkcie). čísla), ktorý nemá aspoň jeden kladný prvok) ...
Keďže nájdené základné riešenie neobsahuje negatívne zložky, je prípustné.
6. fáza: kontrola optimálnosti.
Nájdené základné riešenie nie je optimálne, pretože podľa kritéria optimality (funkcia 4) by v riadku účelovej funkcie nemali byť žiadne negatívne prvky (voľné číslo tohto riadku sa pri posudzovaní tohto prvku neberie do úvahy) . Preto podľa algoritmu simplexovej metódy prejdeme do 8. fázy.
Keďže nájdené základné riešenie je prípustné, hľadanie rozlišovacieho stĺpca sa uskutoční podľa nasledujúcej schémy: určíme stĺpce so zápornými prvkami v riadku účelovej funkcie (okrem stĺpca voľných čísel). Podľa tabuľky 5.3 existujú dva takéto stĺpce: stĺpec „ x1"A stĺpec" x2". Z týchto stĺpcov sa vyberie ten, ktorý obsahuje najmenší prvok v riadku účelovej funkcie. Ona bude riešiť. reproduktor" x2"Obsahuje najmenší prvok (–3) v porovnaní so stĺpcom" x1
Na určenie rozlišovacej čiary nájdeme kladné hodnotiace pomery voľných čísel k prvkom rozlišovacieho stĺpca, pričom za povolenú sa berie priamka, ktorá zodpovedá najmenšiemu kladnému hodnotiacemu pomeru.
Tabuľka 5.4
Zdrojová simplexná tabuľka
V tabuľke 5.4 najmenší kladný odhadovaný pomer zodpovedá riadku „ x5“, Preto to bude vyriešené.
Prvok umiestnený v priesečníku povoľovacieho stĺpca a povoľovacej čiary je akceptovaný ako povoľujúci. V našom príklade ide o prvok umiestnený na priesečníku čiary “ x5"A stĺpce" x2».
Rozlišovací prvok zobrazuje jednu základnú a jednu voľnú premennú, ktoré je potrebné v simplexnej tabuľke prehodiť, aby sa prešlo na nové „vylepšené“ základné riešenie. V tomto prípade ide o premenné x5 a x2, v novej simplexnej tabuľke (tabuľka 5.5) ich prehodíme.
9.1. Transformácia prvkov rozlíšenia.
Permisívny prvok tabuľky 5.4 sa transformuje takto:
![]()
Získaný výsledok zapíšeme do podobnej bunky v tabuľke 5.5.
9.2. Preveďte reťazec rozlíšenia.
Prvky rozlišovacej čiary tabuľky 5.4 delíme rozlišovacím prvkom tejto simplexnej tabuľky, výsledky zapadajú do podobných buniek novej simplexnej tabuľky (tabuľka 5.5). Transformácie prvkov rozlišovacej čiary sú uvedené v tabuľke 5.5.
9.3. Konverzia stĺpca rozlíšenia.
Prvky rozlišovacieho stĺpca tabuľky 5.4 sa delia rozlišovacím prvkom danej simplexnej tabuľky a výsledok sa berie s opačným znamienkom. Získané výsledky zapadajú do podobných buniek novej simplexnej tabuľky (tabuľka 5.5). Transformácie prvkov rozlišovacej kolóny sú uvedené v tabuľke 5.5.
9.4. Preveďte zvyšok prvkov simplexnej tabuľky.
Transformácia zostávajúcich prvkov simplexnej tabuľky (tj prvkov nenachádzajúcich sa v rozlišovacom riadku a rozlišovacom stĺpci) sa vykonáva podľa pravidla "obdĺžnik".
Zvážte napríklad transformáciu prvku umiestneného na priesečníku reťazca " x3"A stĺpec" ", budeme ho konvenčne označovať ako" x3". V tabuľke 5.4 mentálne nakreslite obdĺžnik, ktorého jeden vrchol sa nachádza v bunke, ktorej hodnotu transformujeme (to znamená v bunke „ x3»), A druhý (diagonálny vrchol) je v bunke s rozlišovacím prvkom. Ďalšie dva vrcholy (druhá uhlopriečka) sú jednoznačne určené. Potom transformovaná hodnota bunky " x3"Bude sa rovnať predchádzajúcej hodnote tejto bunky mínus zlomok, v menovateli ktorého je rozlišovací prvok (z tabuľky 5.4), a v čitateli súčin dvoch ďalších nepoužitých vrcholov, tj:
« x3»: .
Hodnoty ostatných buniek sa transformujú podobne:
« x3 x1»: ;
« x4»: ![]() ;
;
« x4 x1»: ;
« x6»: ![]() ;
;
« x6 x1»: ;
«»: ![]() ;
;
« x1»: ![]() .
.
V dôsledku týchto transformácií bola získaná nová simplexná tabuľka (tabuľka 5.5).
II iterácia:
Fáza 1: zostavenie simplexnej tabuľky.
Tabuľka 5.5
Simplexný stôlII iterácií
Odhadovaný vzťah |
||||
| ||||
|
|
2. fáza: stanovenie základného roztoku.
V dôsledku simplexných transformácií sa získalo nové základné riešenie (tabuľka 5.5):
Ako vidíte, pri tomto základnom riešení je hodnota účelovej funkcie = 15, čo je viac ako pri predchádzajúcom základnom riešení.
Nejednotnosť systému obmedzení podľa atribútu 1 v tabuľke 5.5 nebola zistená.
4. fáza: kontrola obmedzenosti cieľovej funkcie.
Neohraničenosť účelovej funkcie v súlade so znakom 2 v tabuľke 5.5 nebola odhalená.
5. etapa: kontrola prípustnosti nájdeného základného riešenia.
Nájdené základné riešenie podľa znaku 4 nie je optimálne, keďže riadok účelovej funkcie simplexovej tabuľky (tabuľka 5.5) obsahuje záporný prvok: –2 (voľné číslo tohto riadku sa pri uvažovaní neberie do úvahy). vlastnosť). Preto ideme do fázy 8.
8. fáza: určenie rozlišovacieho prvku.
8.1. Definícia stĺpca rozlíšenia.
Nájdené základné riešenie je prípustné, v riadku účelovej funkcie definujeme stĺpce so zápornými prvkami (okrem stĺpca voľných čísel). Podľa tabuľky 5.5 je takýmto stĺpcom iba jeden stĺpec: „ x1". Preto to akceptujeme ako povolené.
8.2. Určenie reťazca povolenia.
Podľa získaných hodnôt kladných hodnotiacich pomerov v tabuľke 5.6 je minimom pomer zodpovedajúci čiare „ x3". Preto to akceptujeme ako povolené.
Tabuľka 5.6
Simplexný stôlII iterácií
Odhadovaný vzťah |
||||
3/1 = 3 - min |
||||
Fáza 9: transformácia simplexnej tabuľky.
Simplexné transformácie tabuliek (tabuľky 5.6) sa vykonávajú rovnakým spôsobom ako v predchádzajúcej iterácii. Výsledky transformácií prvkov simplexnej tabuľky sú uvedené v tabuľke 5.7.
III iterácia
Na základe výsledkov simplexných transformácií predchádzajúcej iterácie zostavíme novú simplexnú tabuľku:
Tabuľka 5.7
Simplexný stôlIII iterácií
Odhadovaný vzťah |
||||
| ||||
|
|
2. fáza: stanovenie základného roztoku.
V dôsledku simplexných transformácií sa získalo nové základné riešenie (tabuľka 5.7):
3. fáza: kontrola konzistencie systému obmedzení.
Nejednotnosť systému obmedzení podľa atribútu 1 v tabuľke 5.7 nebola zistená.
4. fáza: kontrola obmedzenosti cieľovej funkcie.
Neohraničenosť účelovej funkcie v súlade so znakom 2 v tabuľke 5.7 nebola odhalená.
5. etapa: kontrola prípustnosti nájdeného základného riešenia.
Nájdené základné riešenie podľa atribútu 3 je prípustné, pretože neobsahuje negatívne zložky.
6. fáza: kontrola optimálnosti nájdeného základného riešenia.
Nájdené základné riešenie podľa znaku 4 nie je optimálne, keďže riadok účelovej funkcie simplexovej tabuľky (tabuľka 5.7) obsahuje záporný prvok: –3 (voľné číslo tohto riadku sa pri uvažovaní neberie do úvahy). vlastnosť). Preto ideme do fázy 8.
8. fáza: určenie rozlišovacieho prvku.
8.1. Definícia stĺpca rozlíšenia.
Nájdené základné riešenie je prípustné, v riadku účelovej funkcie definujeme stĺpce so zápornými prvkami (okrem stĺpca voľných čísel). Podľa tabuľky 5.7 je takýmto stĺpcom iba jeden stĺpec: „ x5". Preto to akceptujeme ako povolené.
8.2. Určenie reťazca povolenia.
Podľa získaných hodnôt kladných hodnotiacich pomerov v tabuľke 5.8 je minimom pomer zodpovedajúci čiare „ x4". Preto to akceptujeme ako povolené.
Tabuľka 5.8
Simplexný stôlIII iterácií
Odhadovaný vzťah |
||||
5/5 = 1 - min |
||||
Fáza 9: transformácia simplexnej tabuľky.
Simplexné transformácie tabuliek (tabuľka 5.8) sa vykonávajú rovnakým spôsobom ako v predchádzajúcej iterácii. Výsledky transformácií prvkov simplexnej tabuľky sú uvedené v tabuľke 5.9.
IV iterácia
Fáza 1: zostavenie nového simplexného stola.
Na základe výsledkov simplexných transformácií predchádzajúcej iterácie zostavíme novú simplexnú tabuľku:
Tabuľka 5.9
Simplexný stôlIV iterácií
Odhadovaný vzťah |
||||
| –(–3/5)=3/5 | |||
–(1/5)=–1/5 | ||||
| –(9/5)=–9/5 | |||
|
| –(–3/5)=3/5 |
2. fáza: stanovenie základného roztoku.
V dôsledku simplexných transformácií sa získalo nové základné riešenie podľa tabuľky 5.9, riešenie je nasledovné:
3. fáza: kontrola konzistencie systému obmedzení.
Nejednotnosť systému obmedzení podľa atribútu 1 v tabuľke 5.9 nebola zistená.
4. fáza: kontrola obmedzenosti cieľovej funkcie.
Neohraničenosť účelovej funkcie v súlade so znakom 2 v tabuľke 5.9 nebola odhalená.
5. etapa: kontrola prípustnosti nájdeného základného riešenia.
Nájdené základné riešenie podľa atribútu 3 je prípustné, pretože neobsahuje negatívne zložky.
6. fáza: kontrola optimálnosti nájdeného základného riešenia.
Nájdené základné riešenie podľa znaku 4 je optimálne, keďže v riadku účelovej funkcie simplexovej tabuľky (tabuľka 5.9) nie sú žiadne negatívne prvky (voľné číslo tohto riadku sa pri posudzovaní tohto znaku neberie do úvahy) .
7. fáza: kontrola alternatívy riešenia.
Nájdené riešenie je jediné, keďže v riadku účelovej funkcie (tabuľka 5.9) nie sú žiadne nulové prvky (voľné číslo tohto riadku sa pri zvažovaní tejto vlastnosti neberie do úvahy).
odpoveď: optimálna hodnota cieľovej funkcie uvažovaného problému = 24, ktorá sa dosiahne pri.
Príklad 5.2. Vyriešte vyššie uvedený problém lineárneho programovania za podmienky, že cieľová funkcia je minimalizovaná:
Riešenie:
ja iterácia:
Fáza 1: vytvorenie počiatočnej simplexnej tabuľky.
Pôvodný problém lineárneho programovania je uvedený v štandardnej forme. Dostaňme ho do jeho kanonickej podoby zavedením ďalšej nezápornej premennej do každého z obmedzení nerovnosti, t.j.

Vo výslednej sústave rovníc berieme ako povolené (základné) premenné x3, x4, x5, x6, potom budú voľné premenné x1,x2... Vyjadrime základné premenné v termínoch voľných.
Jedna z metód riešenia optimalizačných problémov ( zvyčajne spojené s hľadaním minima alebo maxima) sa nazýva lineárne programovanie. Simplexná metóda zahŕňa celú skupinu algoritmov a metód na riešenie problémov lineárneho programovania. Jedna z takýchto metód, zahŕňajúca zaznamenávanie počiatočných údajov a ich prepočítanie do špeciálnej tabuľky, sa nazýva tabuľková simplexová metóda.
Zvážte algoritmus tabuľkovej simplexovej metódy na príklade riešenia výrobná úloha, ktorá sa scvrkáva na nájdenie výrobného plánu, ktorý poskytuje maximálny zisk.
Podnik vyrába 4 druhy výrobkov, spracováva ich na 3 strojoch.
Časové sadzby (min./kus.) Pre spracovanie produktov na strojoch, nastavené maticou A:

Časový fond chodu stroja (min.) je špecifikovaný v matici B:

Zisk z predaja každej jednotky produktu (rubľov / kus) je daný maticou C:

Vypracujte plán výroby, v ktorom bude zisk podniku maximálny.
(1) Označme X1, X2, X3, X4 plánované množstvo produktov každého typu. Potom požadovaný plán: ( X1, X2, X3, X4)
(2) Zapíšme si obmedzenia plánu vo forme sústavy rovníc:

(3) Potom cieľový zisk:
To znamená, že zisk z plnenia plánu výroby by mal byť maximalizovaný.
(4) Na vyriešenie výsledného problému pre podmienený extrém nahradíme systém nerovníc systémom lineárnych rovníc tak, že do neho vložíme ďalšie nezáporné premenné ( X5, X6, X7).

(5) Zoberme si nasledovné základný plán:
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80
(6) Zadáme údaje do simplexný stôl:

V poslednom riadku zadáme koeficienty účelovej funkcie a jej samotnú hodnotu s opačným znamienkom;
(7) Vyberáme v poslednom riadku najväčší (modulo) záporné číslo.
Poďme počítať b = N / Selected_Column_Elements

Medzi vypočítanými hodnotami b vyberte najmenej.
Priesečník vybraného stĺpca a riadku nám poskytne povoľujúci prvok. Základ zmeníme na premennú zodpovedajúcu rozlišovaciemu prvku ( X5 až X1).


a ij (*) = a ij - (A * B / RE)
Ako vidíte, berieme aktuálnu bunku na prepočet a bunku s prvkom rozlíšenia. Tvoria protiľahlé rohy obdĺžnika. Ďalej vynásobíme hodnoty z buniek ostatných 2 rohov tohto obdĺžnika. Táto práca ( A * B) sa delí rozlišovacím prvkom ( RE). A odpočítajte od aktuálne prepočítanej bunky ( a ij) čo sa stalo. Získame novú hodnotu - a ij (*).

(9) Znova skontrolujte posledný riadok ( c) na prítomnosť záporných čísel... Ak tam nie sú, našiel sa optimálny plán, pokračujeme do poslednej fázy riešenia problému. Ak existuje, plán ešte nie je optimálny a simplexnú tabuľku je potrebné znova prepočítať.
Keďže v poslednom riadku máme opäť záporné čísla, spustíme novú iteráciu výpočtov.


(10) Keďže v poslednom riadku nie sú žiadne negatívne prvky, znamená to, že sme našli optimálny plán výroby! Totiž: vyrobíme tie produkty, ktoré sa presunuli do stĺpca Základ - X1 a X2. Poznáme zisk z produkcie každej jednotky produkcie ( matica C). Zostáva vynásobiť zistené objemy výroby výrobkov 1 a 2 so ziskom o 1 kus, dostaneme konečný ( maximálne! ) zisk pre daný plán výroby.
ODPOVEĎ:
X1 = 32 ks, X2 = 20 ks, X3 = 0 ks, X4 = 0 ks.
P = 48 * 32 + 33 * 20 = 2 196 rubľov.
Galyautdinov R.R.
© Kopírovanie materiálu je povolené len vtedy, ak existuje priamy hypertextový odkaz na
Univerzálna metóda riešenia úloh LP sa nazýva simplexná metóda. Aplikácia tejto metódy a jej najbežnejšia modifikácia - dvojfázová simplexová metóda.
Grafickou metódou riešenia úloh LP sme vlastne vybrali z množiny vrcholov patriacich k hranici množiny riešení sústavy nerovníc taký vrchol, v ktorom hodnota účelovej funkcie dosiahla maximum (minimum). V prípade dvoch premenných je táto metóda úplne intuitívna a umožňuje rýchlo nájsť riešenie problému.
Ak sú v probléme tri alebo viac premenných a v reálnych ekonomických problémoch je to presne taká situácia, je ťažké si predstaviť oblasť riešení systému obmedzení. Takéto úlohy sa riešia pomocou simplexná metóda alebo metódou postupného zlepšovania. Myšlienka metódy je jednoduchá a je nasledovná.
Podľa určitého pravidla sa nájde počiatočný referenčný plán (niektorý vrchol obmedzujúcej oblasti). Kontroluje sa, či je plán optimálny. Ak áno, problém je vyriešený. Ak nie, tak prejdite na ďalší vylepšený plán – na ďalší vrchol. hodnota účelovej funkcie na tomto pláne (v tomto vrchole) je samozrejme lepšia ako v predchádzajúcom. Algoritmus prechodu sa vykonáva pomocou nejakého výpočtového kroku, ktorý je pohodlne napísaný vo forme tabuliek, tzv. simplexné stoly ... Keďže počet vrcholov je konečný, tak v konečnom počte krokov prichádzame k optimálnemu riešeniu.
Uvažujme o simplexnej metóde pomocou konkrétneho príkladu problému zostavenia plánu.
Všimnite si znova, že simplexná metóda je použiteľná na riešenie kanonických problémov LP zredukovaných na špeciálnu formu, t. j. so základom, kladnými pravými stranami a objektívnou funkciou vyjadrenou v termínoch nezákladných premenných. Ak sa úloha nezredukuje na špeciálny formulár, sú potrebné ďalšie kroky, o ktorých budeme hovoriť neskôr.
Zoberme si problém výrobného plánu, ktorý predtým postavil model a zredukoval ho na špeciálnu formu.
Úloha.
Na výrobu produktov A a V sklad môže uvoľniť najviac 80 jednotiek surovín. Navyše na výrobu produktu A spotrebúvajú sa dve jednotky a produkty V- jedna jednotka surovín. Je potrebné plánovať výrobu tak, aby bol zabezpečený čo najväčší zisk produktov A je potrebné vyrobiť nie viac ako 50 kusov a výrobkov V- nie viac ako 40 ks. Navyše zisk z predaja jedného produktu A- 5 rubľov a od V- 3 ruble.
Zostavme matematický model, označujúci pre X 1 počet výrobkov A v pláne, za X 2 - počet produktov V... potom bude systém obmedzení vyzerať takto:
x 1 ≤ 50
x 2 ≤ 40
2x 1 + x 2 ≤ 80
x 1 ≥ 0, x 2 ≥ 0
5x 1 + 3x 2 → max
Prenesme problém do kanonickej podoby zavedením ďalších premenných:
x 1 + x 3 = 50
x 2 + x 4 = 40
2x 1 + x 2 + x 5 = 80
x 1 ≥ 0, x 2 ≥ 0
5x 1 + 3x 2 → max
-F = -5x 1 - 3x 2 → min.
Tento problém má špeciálnu formu (so základom, pravé strany sú nezáporné). Dá sa to vyriešiť simplexnou metódou.
jaetapa. Zápis úlohy do simplexnej tabuľky. Existuje vzájomná zhoda medzi systémom obmedzení problému (3.10) a simplexnou tabuľkou. V tabuľke je toľko riadkov, koľko je rovnosti v systéme obmedzení, a toľko stĺpcov, koľko je voľných premenných. Základné premenné vypĺňajú prvý stĺpec, voľné premenné - horný riadok tabuľky. Spodný riadok sa nazýva indexový riadok, obsahuje koeficienty premenných v účelovej funkcii. Na začiatku sa do pravého dolného rohu zapíše 0, ak vo funkcii nie je voľný termín; ak existuje, zapíšeme ho s opačným znamienkom. Na tomto mieste (v pravom dolnom rohu) bude hodnota účelovej funkcie, ktorá by pri prechode z jednej tabuľky na druhú mala narásť v module. Náš systém obmedzení teda zodpovedá tabuľke 3.4 a môžeme prejsť do II. fázy riešenia.
Tabuľka 3.4
|
základná línia |
zadarmo |
||
IIetapa... Kontrola optimálnosti plánu podpory.
Táto tabuľka 3.4 zodpovedá nasledujúcemu základnému plánu:
(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).
Voľné premenné X 1 , X 2 sa rovnajú 0; X 1 = 0, X 2 = 0. A základné premenné X 3 , X 4 , X 5 preberať hodnoty X 3 = 50, X 4 = 40, X 5 = 80 - zo stĺpca voľných členov. Hodnota objektívnej funkcie:
-F = - 5X 1 - 3X 2 = -50 - 30 = 0.
Našou úlohou je skontrolovať, či je daný základný plán optimálny. na to musíte zobraziť indexový riadok - riadok účelovej funkcie F.
Možné sú rôzne situácie.
1. V indexe F-string nemá žiadne negatívne prvky. To znamená, že plán je optimálny, môžete si napísať riešenie problému. Účelová funkcia dosiahla svoju optimálnu hodnotu rovnajúcu sa číslu v pravom dolnom rohu branej s opačným znamienkom. Prechádzame do štádia IV.
2. Riadok indexu obsahuje aspoň jeden záporný prvok, ktorého stĺpec neobsahuje kladné. Potom dospejeme k záveru, že účelová funkcia F→ ∞ neobmedzene klesá.
3. Riadok indexu obsahuje záporný prvok s aspoň jedným kladným prvkom vo svojom stĺpci. Potom prejdeme do ďalšej fázy III. prepočítanie tabuľky, zlepšenie základnej línie.
IIIetapa... Zlepšenie základnej línie.
Z prvkov negatívneho indexu F-Riadky si vyberú najväčší modul, zavolajú príslušné rozlíšenie stĺpcov a označia "".
Pre výber rozlišovacieho riadku je potrebné vypočítať pomery prvkov stĺpca voľného člena iba Komu pozitívne permisívne stĺpové prvky. Zo získaných vzťahov vyberte minimum. Príslušný prvok, pri ktorom sa dosiahne minimum, sa nazýva rozlišovací prvok. Zvýrazníme ho štvorčekom.
V našom príklade je prvok 2 povolený. Čiara zodpovedajúca tomuto prvku sa nazýva aj rozlišovacia (tabuľka 3.5).
Tabuľka 3.5

Po výbere rozlišovacieho prvku prepočítame tabuľku podľa pravidiel:
1. V novej tabuľke rovnakých rozmerov ako doteraz sú premenné rozlišovacieho riadku a stĺpca prehodené, čo zodpovedá prechodu na nový základ. V našom príklade: X 1 sa zaraďuje do základu, namiesto toho X 5, ktorý opúšťa základ a je teraz zadarmo (tabuľka 3.6).
Tabuľka 3.6
2. Namiesto rozlišovacieho prvku 2 zapíšte jeho prevrátené číslo ½.
3. Prvky rozlišovacej čiary sú rozdelené rozlišovacím prvkom.
4. Prvky rozlišovacieho stĺpca sú rozdelené rozlišovacím prvkom a zapísané s opačným znamienkom.
5. Na vyplnenie zvyšných prvkov tabuľky 3.6 prepočítame podľa pravidla obdĺžnika. Predpokladajme, že chceme počítať prvok na pozícii 50.
Tento prvok mentálne spojíme s riešiacim, nájdeme súčin, odčítame súčin prvkov umiestnených na druhej uhlopriečke výsledného obdĺžnika. Rozdiel delíme rozlišovacím prvkom.
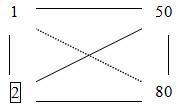
Takže, . Napíšeme 10 na miesto, kde bolo 50. Podobne:
, ![]() , ,
, , ![]() .
.
Tabuľka 3.7

Máme novú tabuľku 3.7, základnými premennými sú teraz premenné (x 3, x 4, x 1). Hodnota objektívnej funkcie sa stala rovnou -200, t.j. poklesla. Aby sme skontrolovali optimálnosť tohto základného riešenia, je potrebné opäť prejsť na II. Proces je samozrejme konečný, kritériá zastavenia sú body 1 a 2 II.
Riešenie problému dotiahneme až do konca. Ak to chcete urobiť, skontrolujte riadok indexu a keď v ňom uvidíte záporný prvok -½, zavolajte rozlíšenie zodpovedajúceho stĺpca a podľa fázy III prepočítajte tabuľku. Po zostavení vzťahov a zvolení medzi nimi minima = 40 sme určili rozlišovací prvok 1. Teraz vykonáme prepočet podľa pravidiel 2-5.
Tabuľka 3.8
Po prepočítaní tabuľky sa ubezpečíme, že v riadku indexu nie sú žiadne negatívne prvky, takže problém je vyriešený, základný plán je optimálny.
IVetapa... Napísanie optimálneho riešenia.
Ak sa simplexová metóda zastavila podľa bodu 1 etapy II, riešenie problému je napísané nasledovne. Základné premenné nadobúdajú hodnoty stĺpca voľného člena, resp. V našom príklade X 3 = 30, X 2 = 40, X 1 = 20. Voľné premenné sú 0, X 5 = 0, X 4 = 0. Účelová funkcia nadobúda hodnotu posledného prvku stĺpca voľných členov s opačným znamienkom: - F = -220 → F= 220, v našom príklade bola funkcia skúmaná na min a na začiatku F→ max, takže v skutočnosti sa označenie zmenilo dvakrát. takze X* = (20, 40, 30, 0, 0), F* = 220. Odpoveď na problém:
Je potrebné zahrnúť 20 produktov typu A, 40 produktov typu B, pričom zisk bude maximálny a bude sa rovnať 220 rubľov.
Na konci tejto časti uvádzame blokovú schému algoritmu simplexnej metódy, ktorá presne opakuje kroky, ale možno pre niektorých čitateľov bude vhodnejšie ju použiť, pretože šípky označujú jasný smer činnosti.
Odkazy nad obdĺžnikmi vo vývojovom diagrame ukazujú, do ktorého štádia alebo článku patrí príslušná transformačná skupina. pravidlo na nájdenie počiatočného základného plánu bude formulované v článku 3.7.

Príklad. Vyriešte nasledujúci problém LP v kanonickej forme pomocou simplexnej metódy.
f (x) = x 1 + 9x 2 + 5x 3 + 3x 4 + 4x 5 + 14x 6 → min
x 1 + x 4 = 20
x 2 + x 5 = 50
x 3 + x 6 = 30
x 4 + x 5 + x 6 = 60
x i ≥ 0, i = 1, ..., 6
Hovorí sa, že problém LP má kanonickú formu, ak všetky obmedzenia (okrem podmienok nezápornosti premenných) majú formu rovnosti a všetky voľné členy sú nezáporné. Takže máme problém v kanonickej forme.
Myšlienka simplexovej metódy je nasledovná. Najprv musíte nájsť nejaký (počiatočný) vrchol mnohostenu realizovateľných riešení (počiatočné realizovateľné základné riešenie). Potom musíte skontrolovať optimálnosť tohto riešenia. Ak je to optimálne, riešenie sa našlo; ak nie, prejdite na iný vrchol polytopu a znova skontrolujte optimálnosť. Vzhľadom na konečnosť vrcholov mnohostenu (dôsledok konečnosti obmedzení úlohy LP) v konečnom počte „krokov“ nájdeme požadovaný minimálny alebo maximálny bod. Treba si uvedomiť, že pri prechode z jedného vrcholu do druhého hodnota účelovej funkcie klesá (v úlohe pre minimum) alebo stúpa (v úlohe pre maximum).
Myšlienka simplexovej metódy je teda založená na troch vlastnostiach problému LP.
Riešenie. Na nájdenie východiskového realizovateľného základného riešenia, t.j. na určenie základných premenných treba systém (5.6) zredukovať na "diagonálny" tvar. Aplikovaním Gaussovej metódy (metóda postupnej eliminácie neznámych) dostaneme z (5.6):
x 2 + x 1 + x 3 = 40
x 4 + x 1 = 20
x 5 - x 1 - x 3 = 10
x 6 + x 3 = 30
Preto sú základné premenné x 2, x 4, x 5, x 6, priradíme im hodnoty rovné voľným členom zodpovedajúcich reťazcov: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,... Premenné x 1 a x 3 sú nezákladné: x 1 = 0, x 3 = 0.
Zostrojme počiatočné prípustné základné riešenie
x 0 = (0,40,0,20,10,30) (5,9)
Na kontrolu optimálnosti nájdeného riešenia x 0 z účelovej funkcie je potrebné vylúčiť základné premenné (pomocou systému (5.8)) a zostrojiť špeciálnu simplexnú tabuľku.
Po odstránení premenných možno účelovú funkciu pohodlne zapísať ako:
f (x) = -7x 1 - 14x 3 +880 (5,10)
Teraz pomocou (5.8) - (5.10) zostavíme počiatočnú simplexnú tabuľku: 
Nulový riadok obsahuje koeficienty s opačným znamienkom zodpovedajúcich premenných pre účelovú funkciu. Kritérium optimality (pre problém hľadania minima): prípustné základné riešenie ( x 0) je optimálny, ak nulový riadok neobsahuje ani jedno striktne kladné číslo (nepočítajúc hodnotu účelovej funkcie (880)). Toto pravidlo platí aj pre nasledujúce iterácie (tabuľky). Prvky nultého riadku sa budú nazývať odhady stĺpcov.
Takže počiatočné prípustné základné riešenie (5.9) nie je optimálne: 7>0, 14>0
.
Nulový stĺpec obsahuje hodnoty základných premenných. Musia byť nezáporné (pozri rovnicu (5.7)). Od prvého do štvrtého riadku sú zapísané koeficienty premenných zo systému (5.8).
Pretože x 0 nie je optimálny, potom musíte prejsť na iný vrchol mnohostenu realizovateľných riešení (zostrojiť nový b.d.). Aby ste to dosiahli, musíte nájsť pivot a vykonať určitú transformáciu (jednoduchá transformácia).
Najprv nájdeme vodiaci prvok tabuľky, ktorý stojí na priesečníku vodiaceho stĺpca (stĺpec s najvyšším kladným hodnotením) a vodiaceho riadku (riadok zodpovedajúci minimálnemu pomeru prvkov nultého stĺpca k zodpovedajúce prvky (prísne pozitívne) vedúceho stĺpca).
V tabuľke 1 je prvý stĺpec tretí stĺpec a prvý riadok je štvrtý riadok (min (40 / 1,30 / 1) = 30/1) sú označené šípkami a vodiaci prvok je označený krúžkom. Hostiteľ označuje, že základná premenná x 6 je potrebné nahradiť nie základným x 3... Potom budú nové základné premenné x 2, x 3, x 4, x 5, a nezákladné - x 1, x 6,... To znamená prechod na nový vrchol mnohostenu realizovateľných riešení. Nájsť súradnicové hodnoty nového realizovateľného základného riešenia x 00 musíte vytvoriť novú simplexnú tabuľku a vykonať v nej základné transformácie:
a) rozdeliť všetky prvky vodiacej čiary vodiacim prvkom, čím sa vodiaci prvok zmení na 1 (pre jednoduchosť výpočtov);
b) pomocou vodiaceho prvku (rovnajúceho sa 1) otočte všetky prvky vodiaceho stĺpca na nuly (podobne ako pri metóde eliminácie neznámych);
V dôsledku toho sa hodnoty nových základných premenných získajú v nulovom stĺpci x 2, x 3, x 4, x 5,(pozri tabuľku 2) - základné komponenty nového vrcholu x 00(nezákladné komponenty x 1 = 0, x 6 = 0,).

Ako ukazuje tabuľka 2, nové základné riešenie x 00 = (0,10,30,20,40,0) neoptimálna (nulová čiara má nezáporné skóre 7). Preto s pivotovým prvkom 1 (viď tabuľka 2) zostavíme nový simplexný stôl, t.j. vytvorenie nového realizovateľného základného riešenia 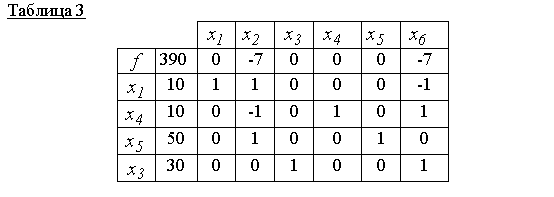
Tabuľka 3 zodpovedá prípustnému základnému riešeniu x 000 = (10,0,30,10,50,0) a je to optimálne, pretože v nulovom riadku nie sú žiadne kladné hodnotenia. Takže f (x 000) = 390 je minimálna hodnota účelovej funkcie.
odpoveď: x 000 = (10, 0, 30, 10, 50, 0)- minimálny bod, f (x 000) = 390.
Otázky na sebaovládanie
Stručná teória
Prostredníctvom označujú obrat 1., 2. a tretieho druhu tovaru, resp.
Potom je účelová funkcia vyjadrujúca zisk:
Obmedzenia materiálnych a peňažných prostriedkov:
Navyše v zmysle problému
Dostaneme nasledujúci problém lineárneho programovania:
Vyplníme simplexnú tabuľku 0. iterácie.
| BP | Simplexné vzťah |
8 | 6 | 4 | 0 | 0 | 0 | 0 | 520 | 16 | 18 | 9 | 1 | 0 | 0 | 65/2 | 0 | 140 | 7 | 7 | 2 | 0 | 1 | 0 | 20 | 0 | 810 | 9 | 2 | 1 | 0 | 0 | 1 | 90 | 0 | -8 | -6 | -4 | 0 | 0 | 0 |
Keďže riešime maximálny problém, prítomnosť záporných čísel v riadku indexu pri riešení maximálneho problému naznačuje, že sme nezískali optimálne riešenie a je potrebné prejsť z tabuľky 0. iterácie na ďalšiu.
Prechod na ďalšiu iteráciu sa vykonáva takto:
Vedúci stĺpec sa zhoduje.
Kľúčový riadok je určený minimálnym pomerom voľných členov a členov vedúceho stĺpca (jednoduché vzťahy):
Na priesečníku kľúčového stĺpca a kľúčového radu nájdeme rozlišovací prvok, teda 7.
Teraz začneme zostavovať 1. iteráciu. Namiesto jednotkového vektora zavedieme vektor.
V novej tabuľke na miesto rozlišovacieho prvku napíšeme 1, všetky ostatné prvky kľúčového stĺpca sa vynulujú. Kľúčové prvky línie sú rozdelené na povoľujúce prvky. Všetky ostatné prvky tabuľky sa vypočítajú podľa pravidla obdĺžnika.
Dostaneme tabuľku 1. iterácie:
| BP | Simplexné vzťah |
8 | 6 | 4 | 0 | 0 | 0 | 0 | 200 | 0 | 2 | 31/7 | 1 | -16/7 | 0 | 1400/31 | 8 | 20 | 1 | 1 | 2/7 | 0 | 1/7 | 0 | 70 | 0 | 630 | 0 | -7 | -11/7 | 0 | -9/7 | 1 | - | 160 | 0 | 2 | -12/7 | 0 | 8/7 | 0 |
Kľúčový stĺpec pre zhody 1. iterácie.
Nájdeme reťazec kľúčov, na tento účel definujeme:
Na priesečníku kľúčového stĺpca a kľúčového radu nájdeme rozlišovací prvok, t.j. 31/7.
Vektor sa odvodí zo základu a vektor sa zavedie.
Dostaneme tabuľku 2. iterácie:
| BP | Simplexné vzťah |
8 | 6 | 4 | 0 | 0 | 0 | 4 | 1400/31 | 0 | 14/31 | 1 | 7/31 | -16/31 | 0 | 8 | 220/31 | 1 | 27/31 | 0 | -2/31 | 9/31 | 0 | 0 | 21730/31 | 0 | -195/31 | 0 | 11/31 | -65/31 | 1 | 7360/31 | 0 | 86/31 | 0 | 12/31 | 8/31 | 0 |
Všetky výrazy v riadku indexu sú nezáporné, takže sa získa nasledovné riešenie problému lineárneho programovania (vypíšeme ho zo stĺpca voľných výrazov):
Preto je potrebné predať 7,1 tisíc rubľov. tovar 1. druhu a 45,2 tisíc rubľov. tovar 3. druhu. Predávať tovar 2. druhu je nerentabilné. V tomto prípade bude zisk maximálny a bude 237,4 tisíc rubľov. Pri implementácii optimálneho plánu bude zvyšok zdroja 3. typu 701 jednotiek.
Ak nepotrebujete pomoc teraz, ale možno ju budete potrebovať v budúcnosti, potom, aby ste nestratili kontakt,