इलेक्ट्रॉनिक गिट्टी और उसका सर्किट कैसे काम करता है
यदि कोई नहीं जानता कि फ्लोरोसेंट लैंप कैसे काम करता है, तो यहां महत्वपूर्ण बिंदु एक विद्युत प्रवाह है, लेकिन इसमें नहीं ...
बाइनरी कोड में संख्या के संकेत को निर्धारित करने के लिए, 0 और 1 का उपयोग किया जाता है। एक शून्य के साथ, "+" कोड अंकित होता है, इकाई को "-" चिह्न द्वारा कोडित किया जाता है।
कंप्यूटिंग में सकारात्मक और नकारात्मक संख्याओं के प्रतिनिधित्व के लिए DIRECT, REVERSE और ADDITIONAL कोड का उपयोग किया जाता है।
सकारात्मक संख्या आगे, रिवर्स और अतिरिक्त कोड को उसी तरह से दर्शाया गया है - साइन बिट में अंक 0 के साथ बाइनरी कोड। उदाहरण के लिए:
ऋणात्मक संख्या प्रत्यक्ष, रिवर्स और अतिरिक्त कोड में एक अलग छवि है।
1. प्रत्यक्ष कोड। अंक 1 को अंक अंक में रखा गया है, और इसके निरपेक्ष मान का बाइनरी कोड संख्या के डिजिटल भाग के अंकों में रखा गया है। उदाहरण के लिए:
2. उल्टा कोड। यह किसी संख्या के निरपेक्ष मान के द्विआधारी कोड के सभी अंकों को प्राप्त करके निकलता है, जिसमें हस्ताक्षर का अंक भी शामिल है: शून्य को उनके द्वारा प्रतिस्थापित किया जाता है, और शून्य द्वारा। उदाहरण के लिए:
3. अतिरिक्त कोड। यह अपनी छोटी श्रेणी के बाद के जोड़ के साथ रिटर्न कोड के गठन का पता लगाता है। उदाहरण के लिए:
आमतौर पर, नकारात्मक दशमलव संख्या स्वचालित रूप से एक रिवर्स या अतिरिक्त बाइनरी कोड में बदल जाती है जब मशीन में प्रवेश किया जाता है और इस रूप में संचालन में संग्रहीत, स्थानांतरित और शामिल होता है। कार से ऐसे नंबर लाने पर, नकारात्मक दशमलव संख्याओं के लिए रिवर्स रूपांतरण।
उदाहरण: नंबर +7, -12, -15, -16 को डायरेक्ट, रिवर्स और अतिरिक्त कोड में प्रस्तुत करें।
अनुवाद करते समय रिवर्स से सीधे में कोड होता है नंबर उलटा.
अनुवाद करते समय अतिरिक्त से सीधे कोड तक है 1) संख्या के अंकों का विलोम, 2)+1 जोड़ा जाता है उल्टे संख्या के निम्न क्रम में।
हस्ताक्षरित संख्याओं पर अंकगणित संचालन
अधिकांश कंप्यूटरों में, घटाव ऑपरेशन का उपयोग नहीं किया जाता है। इसके बजाय, उलटा या अतिरिक्त कोड का जोड़ घटाया और घटाया जाता है। यह आपको ALU के डिजाइन को सरल बनाने की अनुमति देता है।
रिवर्स कोड जोड़ना . यहाँ, A और B संख्याओं को जोड़ने पर चार मुख्य और दो विशेष मामले हैं:
यदि परिणाम एक शून्य चिह्न ("1" के साथ) प्राप्त होता है, तो परिणाम आवश्यक है डायरेक्ट कोड में कन्वर्ट !!!
1. A और B सकारात्मक हैं। संक्षेप में, सभी अंक जोड़े जाते हैं, जिसमें हस्ताक्षर का अंक भी शामिल है। चूंकि सकारात्मक शब्दों के संकेत अंक शून्य हैं, इसलिए राशि चिन्ह का अंक भी शून्य है। उदाहरण के लिए:

सही परिणाम मिला।
2. A धनात्मक है, A की तुलना में B नकारात्मक है और परिमाण में पूर्ण है। | ए |< |B|
उदाहरण के लिए:
यदि परिणाम "1" के साथ ऋण चिह्न के साथ प्राप्त किया जाता है, तो परिणाम को एक प्रत्यक्ष कोड में परिवर्तित किया जाना चाहिए !!!
सही परिणाम रिवर्स कोड में प्राप्त होता है। प्रत्यक्ष कोड में अनुवाद करते समय, परिणाम के डिजिटल हिस्से के बिट्स उल्टे हो जाते हैं: 1 0000111 = -7 10।
3. ए सकारात्मक है, बी नकारात्मक है और ए की तुलना में पूर्ण मूल्य में कम है। | ए | \u003e | बी |
उदाहरण के लिए:

कंप्यूटर शुरू में प्राप्त गलत परिणाम को सही करता है (7 के बजाय 6) यूनिट ट्रांसफर कम रैंक राशि के लिए साइन रैंक से।
4. ए और बी नकारात्मक हैं। उदाहरण के लिए:

कंप्यूटर का प्रारंभिक गलत परिणाम (संख्या -10 10 के व्युत्क्रम कोड के बजाय नंबर -11 10 का उलटा कोड) को इकाई से साइन बिट से राशि के निचले अंक में स्थानांतरित करके ठीक किया जाता है। परिणाम को एक प्रत्यक्ष कोड में तब्दील करते समय, संख्या के डिजिटल भाग के बिट्स उल्टे हो जाते हैं: 1 0001010 = -10 10।
जोड़ते समय, एक स्थिति उत्पन्न हो सकती है जब ऑपरेशन के परिणाम के उच्च-क्रम बिट्स इसके लिए आवंटित मेमोरी क्षेत्र में फिट नहीं होते हैं। इस स्थिति को कहा जाता है संख्या प्रारूप के अंक ग्रिड का अतिप्रवाह। अतिप्रवाह का पता लगाने और कंप्यूटर में त्रुटि के बारे में सूचित करने के लिए विशेष उपकरणों का उपयोग किया जाता है। नीचे दो संभावित अतिप्रवाह मामले हैं।
5. A और B सकारात्मक हैं, A + B का योग 2 से अधिक या उसके बराबर है n-1 , जहाँ n संख्या स्वरूप के अंकों की संख्या है (एकल-बाइट प्रारूप के लिए, n = 8, 2 n-1 = 27 = 128)। अतिप्रवाह विकल्प।
उदाहरण के लिए:
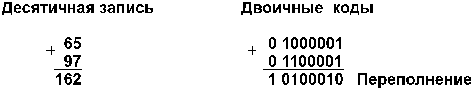
संख्या प्रारूप के डिजिटल भाग के सात अंक पर्याप्त नहीं है अतः आठ अंकों का योग (162 10 = 10100010 2) समायोजित करें राशि के उच्च बिट साइन बिट में है। यह कारण बनता है योग चिह्न और शर्तों के बेमेलकि थोड़ा अतिप्रवाह का प्रमाण है.
कंप्यूटर में पूर्णांकों का प्रतिनिधित्व।
इंटीजर सबसे सरल संख्यात्मक डेटा हैं जिसके साथ कंप्यूटर संचालित होता है। पूर्णांक के लिए, दो प्रतिनिधित्व हैं: अहस्ताक्षरित (केवल गैर-नकारात्मक पूर्णांक के लिए) और हस्ताक्षरित। यह स्पष्ट है कि नकारात्मक संख्याओं को केवल एक प्रतीकात्मक रूप में दर्शाया जा सकता है। इंटीजर कंप्यूटर में संगृहीत होते हैं निश्चित बिंदु प्रारूप.
अहस्ताक्षरित पूर्णांक प्रकारों में पूर्णांक का प्रतिनिधित्व।
एक अहस्ताक्षरित प्रतिनिधित्व के लिए, सेल के सभी अंकों को संख्या के प्रतिनिधित्व को सौंपा गया है। उदाहरण के लिए, एक बाइट (8 बिट्स) में, 0 से 255 तक के अहस्ताक्षरित संख्याओं का प्रतिनिधित्व किया जा सकता है। इसलिए, यदि यह ज्ञात है कि संख्यात्मक मान गैर-ऋणात्मक है, तो इसे अहस्ताक्षरित मान लेना बेहतर है।
हस्ताक्षरित पूर्णांक प्रकारों में पूर्णांकों का प्रतिनिधित्व।
एक हस्ताक्षरित प्रतिनिधित्व के लिए, सबसे महत्वपूर्ण (बाएं) बिट को नंबर के चिह्न को सौंपा गया है, शेष बिट्स को संख्या को ही। यदि संख्या सकारात्मक है, तो 0 को साइन बिट में रखा गया है, यदि नकारात्मक - 1. उदाहरण के लिए, बाइट में, आप -128 से 127 तक हस्ताक्षरित संख्याओं का प्रतिनिधित्व कर सकते हैं।
प्रत्यक्ष कोड संख्या।
सामान्य रूप "संख्या" - "मान" में एक संख्या का प्रतिनिधित्व, जिसमें सेल के उच्च-क्रम सेल को संकेत को सौंपा गया है, और बाकी - संख्या को बाइनरी सिस्टम में लिखने के लिए कहा जाता है प्रत्यक्ष कोड बाइनरी नंबर। उदाहरण के लिए, 8-बिट सेल के लिए बाइनरी संख्या 1001 और -1001 का प्रत्यक्ष कोड क्रमशः 00001001 और 10001001 है।
एक कंप्यूटर में सकारात्मक संख्याओं को हमेशा एक प्रत्यक्ष कोड का उपयोग करके दर्शाया जाता है। संख्या का प्रत्यक्ष कोड पूरी तरह से मशीन के सेल में संख्या के रिकॉर्ड के साथ मेल खाता है। एक ऋणात्मक संख्या का प्रत्यक्ष कोड केवल साइन बिट की सामग्री द्वारा संबंधित सकारात्मक संख्या के प्रत्यक्ष कोड से भिन्न होता है। लेकिन एक प्रत्यक्ष कोड के माध्यम से नकारात्मक पूर्णांक कंप्यूटर में प्रतिनिधित्व नहीं करते हैं, तथाकथित अतिरिक्त कोड.
अतिरिक्त कोड संख्या।
अतिरिक्त कोड सकारात्मक संख्या इस संख्या के प्रत्यक्ष कोड के बराबर है। ऋणात्मक संख्या m का अतिरिक्त कोड 2 k - | m | |, जहाँ k सेल में अंकों की संख्या है।
जैसा कि पहले ही उल्लेख किया गया है, जब अहस्ताक्षरित प्रारूप में गैर-नकारात्मक संख्याओं का प्रतिनिधित्व करते हैं, तो सेल के सभी अंक संख्या को ही सौंपे जाते हैं। उदाहरण के लिए, एक निरूपित प्रतिनिधित्व के साथ एक बाइट में संख्या 243 = 11110011 लिखना इस तरह दिखेगा:
हस्ताक्षर करें
प्रश्न उठता है: एक अतिरिक्त कोड के रूप में नकारात्मक संख्याएं किस उद्देश्य से लिखी जाती हैं और एक नकारात्मक संख्या के अतिरिक्त कोड को कैसे प्राप्त करें?
अतिरिक्त कोड का उपयोग किया जाता है। अंकगणितीय संचालन के निष्पादन को आसान बनाने के लिए। यदि कंप्यूटर ने सकारात्मक और नकारात्मक संख्याओं के प्रत्यक्ष कोड के साथ काम किया है, तो अंकगणितीय संचालन करते समय कई अतिरिक्त क्रियाएं करना आवश्यक होगा। उदाहरण के लिए, इसके अलावा, दोनों ऑपरेंड के संकेतों की जांच करना और परिणाम के संकेत को निर्धारित करना आवश्यक होगा। यदि वर्ण समान हैं, तो ऑपरेंड के योग की गणना की जाती है और उसी वर्ण को इसे सौंपा जाता है। यदि वर्ण अलग-अलग हैं, तो छोटे को संख्या के बड़े निरपेक्ष मान से घटाया जाता है और उच्च संख्या को परिणाम को सौंपा जाता है। यही है, संख्याओं के इस तरह के प्रतिनिधित्व के साथ (केवल एक प्रत्यक्ष कोड के रूप में), इसके अलावा के संचालन को एक जटिल एल्गोरिथ्म के माध्यम से महसूस किया जाता है। यदि ऋणात्मक संख्याओं को एक अतिरिक्त कोड के रूप में दर्शाया जाता है, तो इसके अतिरिक्त ऑपरेशन, जिसमें एक अलग संकेत शामिल है, को बिटवाइज़ जोड़कर घटा दिया जाता है।
पूर्णांक के कंप्यूटर प्रतिनिधित्व के लिए, एक, दो या चार बाइट्स आमतौर पर उपयोग किए जाते हैं, अर्थात्, मेमोरी सेल में क्रमशः आठ, सोलह या बत्तीस बिट्स शामिल होंगे।
एक ऋणात्मक संख्या का एक अतिरिक्त कोड प्राप्त करने के लिए एल्गोरिदम।
एक ऋणात्मक संख्या का अतिरिक्त k- अंकीय कोड प्राप्त करने के लिए, आपको चाहिए
1. ऋणात्मक संख्या मापांक को k बाइनरी अंकों में प्रत्यक्ष कोड द्वारा दर्शाया जाना चाहिए;
2. सभी बिट्स के मूल्य को उल्टा करें: सभी शून्य को अपने साथ बदलें, और लोगों को शून्य के साथ बदलें (इस प्रकार, मूल संख्या का एक k- बिट रिटर्न कोड प्राप्त होता है);
बाइनरी एन्कोडिंग के सिद्धांतों को कंप्यूटर के संचालन के सिद्धांतों में शामिल किया गया है: सभी डेटा को किसी तरह से बाइनरी संख्याओं के रूप में दर्शाया गया है। डेटा पर तार्किक और अंकगणितीय संचालन करने के लिए बाइनरी नंबर के कोड आवश्यक हैं।
"नंबर सिस्टम" लेख में हमने केवल सकारात्मक संख्याओं पर विचार किया। जब उनके प्रारूप में एक संकेत के साथ द्विआधारी संख्या लिखते हैं, तो दो फ़ील्ड प्रदान करना आवश्यक है: एक संख्या के संकेत को परिभाषित करने वाला एक क्षेत्र, और एक संख्या के मापांक की विशेषता वाला क्षेत्र। संख्या के संकेत के लिए एक विशेष साइन बिट (बाइनरी बिट) आरक्षित है। शेष अंक संख्या के मापांक को निर्धारित करते हैं। साइन बिट संख्या के मापांक के बाईं ओर दिया गया है, "बिट" साइन बिट के शून्य मान के समान है, और "-" साइन - एक।
कंप्यूटर के विकास के इतिहास में संकेत संख्याओं का प्रतिनिधित्व करने के लिए तीन मुख्य विकल्पों का उपयोग किया गया है:
तीनों संहिताओं में, सकारात्मक संख्याएं समान दिखती हैं। रिवर्स और अतिरिक्त कोड चिंता में नकारात्मक संख्या लिखने के रूप में अंतर केवल मॉड्यूल एक संख्या का प्रतिनिधित्व करता है, और साइन बिट के कोडिंग विधि और स्थान अपरिवर्तित रहते हैं।
प्रत्यक्ष कोड प्रतिनिधित्व प्रणाली में, संख्या में साइन कोड और संख्या के मापांक होते हैं, दोनों को अलग-अलग संसाधित किया जाता है।
सही अंशों के लिए प्रत्यक्ष कोड के उदाहरण:
पूर्णांक के लिए प्रत्यक्ष कोड के उदाहरण:
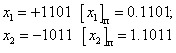
प्रत्यक्ष कोड में संख्याओं के प्रतिनिधित्व में एक महत्वपूर्ण खामी है - अलग-अलग संकेतों के साथ संख्याओं का औपचारिक योग एक गलत परिणाम देता है। उदाहरण - दो संख्याओं का जोड़ ![]() और
और ![]() । प्रत्यक्ष कोड में, इन नंबरों का रूप है: और। जाहिर है, परिणाम -2 होना चाहिए, जिसे प्रत्यक्ष कोड में 1.010 लिखा जा सकता है। उसी समय, सीधे जोड़ के साथ हम प्राप्त करते हैं
। प्रत्यक्ष कोड में, इन नंबरों का रूप है: और। जाहिर है, परिणाम -2 होना चाहिए, जिसे प्रत्यक्ष कोड में 1.010 लिखा जा सकता है। उसी समय, सीधे जोड़ के साथ हम प्राप्त करते हैं
वह है, एक मूल्य जो अपेक्षा से काफी अलग है।
प्रत्यक्ष कोड में संख्याओं के सही जोड़ के लिए प्रक्रिया मौजूद है, लेकिन यह बहुत ही बोझिल है। प्रत्यक्ष कोड में एक और खामी है - शून्य के दो अलग-अलग प्रतिनिधित्व हैं, अर्थात् और गणितीय रूप से इसका कोई मतलब नहीं है।
कंप्यूटरों में विख्यात कमियों के कारण, प्रत्यक्ष कोड का उपयोग नहीं किया जाता है, लेकिन रिवर्स और अतिरिक्त कोड।
इन कोडिंग प्रणालियों में, साइन बिट और कोडिंग विधि का स्थान प्रत्यक्ष कोडिंग के समान ही रहता है। हालांकि, साइन बिट को अब एक अलग के रूप में नहीं माना जाता है, लेकिन संख्या के अभिन्न अंग के रूप में माना जाता है, संख्या मॉड्यूल के अंकों के समान और उनके साथ।
नकारात्मक बाइनरी संख्याओं के लिए, एक व्युत्क्रम कोड प्राप्त करने की प्रक्रिया इस प्रकार है: एक इकाई को साइन बिट में लिखा जाता है, और प्रत्यक्ष कोड के अंकों में इकाई को शून्य और शून्य के साथ बदल दिया जाता है।
सही अंशों के लिए रिटर्न कोड के उदाहरण:
 .
.
पूर्णांक के लिए रिवर्स कोड के उदाहरण:
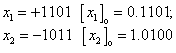 .
.
यह देखना आसान है कि आगे और रिवर्स कोड में सकारात्मक संख्याएं समान दिखती हैं।
हालांकि उलटा कोड विभिन्न संकेतों के साथ संख्याओं के जोड़ और घटाव की समस्या को हल करने की अनुमति देता है, लेकिन इसमें कमियां भी हैं। सबसे पहले, संख्याओं की प्रक्रिया एक दो-चरण प्रक्रिया है, जो इस ऑपरेशन के निष्पादन समय को बढ़ाती है। दूसरे, सीधे कोड में, विपरीत में - शून्य के दो प्रतिनिधित्व: और।
एक नकारात्मक बाइनरी नंबर का अतिरिक्त कोड निम्न नियम के अनुसार बनता है: प्रत्यक्ष कोड के डिजिटल अंकों में, इकाइयों को शून्य के साथ और शून्य को इकाइयों के साथ प्रतिस्थापित किया जाना चाहिए, जिसके बाद एक को निचले क्रम के अंक में जोड़ा जाना चाहिए।
उदाहरण के लिए, संख्या पर विचार करें एक्सजो प्रत्यक्ष कोड में फार्म है:
फिर रिवर्स कोड के रूप में लिखा जा सकता है
![]() .
.
अतिरिक्त कोड के लिए, रिवर्स कोड के निचले क्रम में 1 जोड़ें:
![]() .
.
सही अंशों के लिए अतिरिक्त कोड के उदाहरण:
 .
.
पूर्णांक के लिए अतिरिक्त कोड के उदाहरण:
 .
.
अतिरिक्त कोड में सकारात्मक संख्याएं उसी तरह से लिखी जाती हैं जैसे कि प्रत्यक्ष में। अतिरिक्त कोड में संख्याओं का प्रतिनिधित्व करते समय, शून्य लिखने का केवल एक रूप है: 0.0 ... 00, और शून्य को एक सकारात्मक संख्या माना जाता है, क्योंकि इसका साइन बिट 0 है।
अधिकांश कंप्यूटरों में, अतिरिक्त संख्या में नकारात्मक संख्याओं का प्रतिनिधित्व किया जाता है।
रिवर्स और अतिरिक्त कोड में संख्याओं का जोड़ और घटाव
घटाव को संख्याओं के जोड़ के रूप में किया जाता है, जिनमें से एक नकारात्मक चिन्ह के साथ है।
बीजगणितीय जोड़ को निष्पादित करते समय, अंक चरित्र और मॉड्यूल के अंकों को एक पूरे के रूप में माना जाता है और एक साथ संसाधित किया जाता है। रिवर्स और अतिरिक्त कोड में वरिष्ठ (साइन) अंक से स्थानांतरण को अलग-अलग तरीकों से ध्यान में रखा जाता है। उलटा कोड के मामले में, साइन बिट से ट्रांसफर यूनिट को कम ऑर्डर राशि में जोड़ा जाता है। जब एक अतिरिक्त कोड का उपयोग किया जाता है, तो ट्रांसफर यूनिट को साइन बिट से त्याग दिया जाता है।
उदाहरण 1 संख्याएँ जोड़ें ![]() और
और ![]()
रिवर्स कोड का उपयोग करते समय, हमें मिलता है:
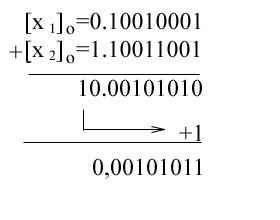
अतिरिक्त कोड का उपयोग करते समय हमें मिलता है:
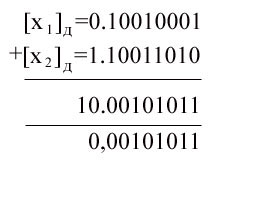
यदि परिणाम का संकेत अंक शून्य है, तो इसका मतलब है कि एक सकारात्मक संख्या प्राप्त हुई है, जो प्रत्यक्ष कोड के समान है। संकेत अंक में एक इकाई का अर्थ है कि परिणाम नकारात्मक है और इसकी प्रविष्टि उस कोड के प्रतिनिधित्व से मेल खाती है जिसमें ऑपरेशन किया गया था।
मुख्य लेख: विघटनकारी सामान्य रूप
सरल संयोजन या संयोजक को चर के कुछ परिमित समुच्चय या उनकी अवगुण कहा जाता है, और प्रत्येक चर एक से अधिक बार नहीं होता है। विघटनकारी सामान्य रूप या वियोगी सामान्य रूप जिसे साधारण संयुग्मन की अव्यवस्था कहा जाता है। प्राथमिक संयोजन
सहीयदि प्रत्येक चर इसमें शामिल है तो एक बार से अधिक (नकारात्मक सहित);
संपूर्णयदि प्रत्येक चर (या इसका निषेध) ठीक 1 बार प्रवेश करता है;
monotonicअगर इसमें वेरिएबल्स का नेगेटिव नहीं है।
उदाहरण के लिए - DNF है।
बिल्कुल सही असहमतिपूर्ण सामान्य रूप या PDNF चर के कुछ दिए गए परिमित सेट के संबंध में, ऐसे DNF को कहा जाता है, जिसमें दिए गए सेट के सभी चर प्रत्येक संयोजन में और उसी क्रम में शामिल होते हैं। उदाहरण के लिए:।
यह सत्यापित करना आसान है कि एक निश्चित DNF प्रत्येक बूलियन फ़ंक्शन से मेल खाती है, और यहां तक कि DNFN समान शून्य के अलावा अन्य फ़ंक्शन के लिए। ऐसा करने के लिए, इस फ़ंक्शन की सत्य तालिका में सभी बूलियन वैक्टर को खोजने के लिए पर्याप्त है, जिस पर इसका मूल्य 1 है, और प्रत्येक ऐसे वेक्टर के लिए एक संयोजन बनाते हैं ![]() कहाँ। इन संयोजनों का विघटन मूल फ़ंक्शन का PDNF है, क्योंकि सभी बूलियन वैक्टर मूल फ़ंक्शन के मूल्यों के साथ मेल खाते हैं। उदाहरण के लिए, निहितार्थ के लिए, परिणाम यह है कि आप को सरल बना सकते हैं।
कहाँ। इन संयोजनों का विघटन मूल फ़ंक्शन का PDNF है, क्योंकि सभी बूलियन वैक्टर मूल फ़ंक्शन के मूल्यों के साथ मेल खाते हैं। उदाहरण के लिए, निहितार्थ के लिए, परिणाम यह है कि आप को सरल बना सकते हैं।
मुख्य लेख: संयोजी सामान्य रूप
संयोजक सामान्य form1 (CNF) को DNF के अनुसार निर्धारित किया जाता है। साधारण अव्यवस्था या एक खंड एक या कई चरों या उनके नकारों के विघटन को कहा जाता है, और प्रत्येक चर एक बार से अधिक नहीं होता है। CNF सरल विघटन का एक संयोजन है।
बिल्कुल सही सामान्य रूप (SKNF), कुछ दिए गए परिमित समुच्चयों के संबंध में, ऐसे CNF कहलाते हैं, जिसमें दिए गए समुच्चय के सभी चर प्रत्येक अव्यवस्था में शामिल होते हैं, और उसी क्रम में। चूंकि (C) CNF और (C) DNF परस्पर दोहरे हैं, CNF के गुण (C) DNF के सभी गुणों को दोहराते हैं, मोटे तौर पर, "बिल्कुल विपरीत"।
एक CNF को नियम के अनुसार कोष्ठक खोलकर उसके समतुल्य DNF में बदला जा सकता है:
जो एक संयोजन के वितरण को अव्यवस्था के संबंध में व्यक्त करता है। इसके बाद, प्रत्येक संयोजन में दोहराए गए चर या उनकी नकारात्मकता को हटाने के लिए आवश्यक है, और उन सभी संयोजनों को भी अस्वीकार करने से जिसमें चर का सामना अपनी उपेक्षा के साथ किया जाता है। इस मामले में, परिणाम आवश्यक रूप से PDNF नहीं होगा, भले ही मूल CNF CNF था। इसी तरह, आप हमेशा डीएनएफ से सीएनएफ में जा सकते हैं। ऐसा करने के लिए, नियम का उपयोग करें
संयुग्मन के संबंध में वितरण की अभिव्यक्ति को व्यक्त करना। परिणाम को ऊपर वर्णित तरीके से परिवर्तित किया जाना चाहिए, "संयोजन" शब्द को "विघटन" के साथ और इसके विपरीत।
16 तार्किक अभिव्यक्तियों के परिवर्तन के नियम: एक-जोड़ी तत्व, निषेध।
तर्क के बीजगणित में, ऐसे कानून हैं जो संबंधों के रूप में लिखे गए हैं। तार्किक कानून किसी को तार्किक अभिव्यक्तियों के समतुल्य (समतुल्य) परिवर्तन करने की अनुमति देते हैं। रूपांतरण को समतुल्य कहा जाता है यदि तार्किक फ़ंक्शन के परिवर्तन के बाद मूल के वास्तविक मूल्य और प्राप्त किए गए, उनमें निहित तार्किक चर के सभी मूल्यों के लिए समान हैं।
सादगी के लिए, हम दो तार्किक चर के लिए तर्क के बीजगणित के बुनियादी कानूनों को प्रस्तुत करते हैं। एकऔर वीये कानून अन्य तार्किक चर पर लागू होते हैं।
1. विरोधाभास का नियम:
2. बहिष्कृत मध्य का नियम:
3. दोहरे निषेध का नियम:
![]()
4. डी मॉर्गन के नियम:
5. पुनरावृत्ति के नियम: ए और ए = ए; ए वी ए = ए; बी एंड बी = बी; बी वी बी = बी।
6. अवशोषण के नियम: एक∨ (ए एंड बी) = ए; A & A (A)∨ बी) = ए।
7. स्थिरांक के बहिष्करण के नियम: एक∨ 1 = 1; एक∨ 0 = ए; ए और 1 = ए; ए और 0 = 0; बी∨ 1 = 1; बी∨ 0 = बी; बी एंड 1 = बी; B & 0 = 0।
8. gluing के नियम:
9. विरोधाभास का नियम: (ए⇔ बी) = (बी)⇔ ए)।
तार्किक चर के लिए, सामान्य गणितीय कानून भी मान्य हैं। सादगी के लिए, हम तीन तार्किक चर के लिए सामान्य गणितीय कानून देते हैं। ए, बी और सी:
1. कम्यूटेटिव कानून: ए और बी = बी एंड ए; एक∨ बी = बी∨ ए
2. सहयोगी कानून: A & (B & C) = (A & B) & C; एक∨ (बी∨ सी) = (ए)∨ बी)∨ सी
3. वितरण संबंधी कानून: ए और (बी)∨ C) = (A & B)∨ (A & C)।
जैसा कि पहले ही उल्लेख किया गया है, तर्क के बीजगणित के नियमों का उपयोग करके, हम उन्हें सरल बनाने के लिए तार्किक अभिव्यक्तियों के समतुल्य परिवर्तनों का उत्पादन कर सकते हैं। तर्क के बीजगणित में, तार्किक संचालन करने के लिए निम्नलिखित नियम (प्राथमिकताएं) समझौते के आधार पर स्थापित किए जाते हैं: संचालन पहले कोष्ठक में किए जाते हैं, फिर निम्नलिखित क्रम में: उलटा (निषेध), संयोजन (और), विघटन (v), निहितार्थ (⇒), समतुल्य। (⇔)
रूपांतरण करें, उदाहरण के लिए, एक तर्क फ़ंक्शन
तर्क के बीजगणित के उपयुक्त कानूनों को लागू करना।
17 तार्किक अभिव्यक्तियों के परिवर्तन के नियम: संयुक्त कानून।
औपचारिक तर्क के नियम
विचारों के बीच सबसे सरल और आवश्यक सच्चे संबंध औपचारिक तर्क के बुनियादी कानूनों में व्यक्त किए जाते हैं। इस तरह के पहचान के नियम, गैर-विरोधाभास, तीसरे को छोड़कर, पर्याप्त कारण हैं।
ये कानून मौलिक हैं क्योंकि तर्क में वे विशेष रूप से महत्वपूर्ण भूमिका निभाते हैं, सबसे आम हैं। वे हमें तार्किक अभिव्यक्तियों को सरल बनाने और निष्कर्ष और प्रमाण बनाने की अनुमति देते हैं। उपरोक्त कानूनों के पहले तीन को अरस्तू द्वारा पहचाना और तैयार किया गया था, और पर्याप्त कारण का कानून - जी। लीबनिज।
पहचान का नियम: एक निश्चित तर्क की प्रक्रिया में, प्रत्येक अवधारणा और निर्णय स्वयं के साथ समान होना चाहिए।
गैर-विरोधाभास का नियम: यह असंभव है कि एक ही समय में एक ही हो और एक ही संबंध में एक ही में निहित न हो। यही है, एक ही समय में कुछ को राज्य करना और इनकार करना असंभव है।
बहिष्कृत मध्य का कानून: दो विरोधाभासी निर्णयों में से, एक सत्य है, दूसरा गलत है और तीसरा नहीं दिया गया है।
पर्याप्त कारण का नियम: प्रत्येक सच्चे विचार को पर्याप्त रूप से प्रमाणित किया जाना चाहिए।
अंतिम कानून कहता है कि किसी वस्तु का प्रमाण ठीक और केवल सच्चे विचारों की पुष्टि करता है। गलत विचारों को साबित नहीं किया जा सकता है। एक अच्छी लैटिन कहावत है: "गलती करना हर व्यक्ति की विशेषता है, लेकिन एक त्रुटि पर जोर देना केवल मूर्ख के लिए अजीब है।" इस कानून का सूत्र नहीं है, क्योंकि इसमें केवल एक सार्थक चरित्र है। सत्य विचार की पुष्टि के लिए तर्क के रूप में, सच्चे निर्णय, तथ्यात्मक सामग्री, सांख्यिकीय डेटा, विज्ञान के नियम, स्वयंसिद्ध, सिद्ध सिद्धांत का उपयोग किया जा सकता है।
वाक्यों के बीजगणित के नियम
कथनों का बीजगणित (तर्क का बीजगणित) गणितीय तर्कशास्त्र की एक शाखा है जो कथनों पर तार्किक संचालन और जटिल कथनों को बदलने के नियमों का अध्ययन करता है।
कई तार्किक समस्याओं को हल करते समय, अक्सर अपनी शर्तों को औपचारिक रूप देकर प्राप्त सूत्रों को सरल बनाना आवश्यक होता है। कथनों के बीजगणित में सूत्रों का सरलीकरण मूल तार्किक कानूनों के आधार पर समकक्ष परिवर्तनों के आधार पर किया जाता है।
प्रस्तावों के बीजगणित (तर्क के बीजगणित) के नियम तनातनी हैं।
कभी-कभी इन कानूनों को प्रमेय कहा जाता है।
बयानों के बीजगणित में, तार्किक कानूनों को समान सूत्रों की समानता के रूप में व्यक्त किया जाता है। कानूनों के बीच ऐसे हैं जिनमें एक चर है।
नीचे दिए गए पहले चार कानून कथनों के बीजगणित के मूल नियम हैं।
पहचान का नियम:
प्रत्येक अवधारणा और निर्णय स्वयं के साथ समान है।
पहचान के कानून का मतलब है कि तर्क की प्रक्रिया में एक विचार को दूसरे के साथ, एक अवधारणा को दूसरे के साथ प्रतिस्थापित करना असंभव है। यदि इस कानून का उल्लंघन किया जाता है, तो तार्किक त्रुटियां संभव हैं।
उदाहरण के लिए, तर्क सही ढंग से वे कहते हैं कि भाषा कीव में लाएगी, और कल मैंने एक स्मोक्ड जीभ खरीदी, इसलिए अब मैं सुरक्षित रूप से कीव जा सकता हूंगलत, क्योंकि पहला और दूसरा शब्द "भाषा" विभिन्न अवधारणाओं को दर्शाता है।
तर्क में: हमेशा के लिए आंदोलन। स्कूल जाना एक आंदोलन है। इसलिए, हमेशा के लिए स्कूल जानाशब्द "आंदोलन" का उपयोग दो अलग-अलग इंद्रियों में किया जाता है (पहला - दार्शनिक अर्थ में - पदार्थ की विशेषता के रूप में, दूसरा - साधारण अर्थ में - अंतरिक्ष में आंदोलन के लिए एक क्रिया के रूप में), जो एक झूठे निष्कर्ष की ओर ले जाता है।
गैर-विरोधाभास का नियम:
एक ही समय में निर्णय और इसकी उपेक्षा सही नहीं हो सकती। वह है, अगर बयान एक- सच है, उसका इनकार नहींगलत होना चाहिए (और इसके विपरीत)। फिर उनका काम हमेशा झूठा होगा।
18 तार्किक कार्यों की विश्लेषणात्मक रिकॉर्डिंग को न्यूनतम करना: कार्नोट मानचित्र विधि।
कार्नो मानचित्र - स्विचिंग (बूलियन) कार्यों को कम करने के लिए एक ग्राफिकल तरीका, बड़े भाव के साथ काम करने की सादगी प्रदान करता है और संभावित दौड़ को समाप्त करता है।
एक ऋणात्मक संख्या का एक अतिरिक्त कोड एक द्विआधारी संख्या (पहले जोड़) के मापांक को सम्मिलित करके और व्युत्क्रम (दूसरे जोड़) में जोड़कर या संख्या को शून्य से घटाकर प्राप्त किया जा सकता है।
एक बाइनरी नंबर का अतिरिक्त कोड (2 के अलावा) इसके 1 के कम से कम महत्वपूर्ण अंक को जोड़कर प्राप्त किया जाता है।
बाइनरी 8-बिट संख्या एक संकेत के साथ अतिरिक्त कोड में ger128 से +127 तक की सीमा में किसी भी पूर्णांक का प्रतिनिधित्व कर सकते हैं। यदि उच्च-क्रम बिट शून्य है, तो शेष 7 अंकों में लिखा जाने वाला सबसे बड़ा पूर्णांक है 2 7 - 1 (\\ डिस्प्लेस्टाइल 2 ^ (7) -1)वह 127 है।
| दशमलव विचार |
बाइनरी प्रतिनिधित्व (8 बिट्स) | ||
|---|---|---|---|
| सीधे | वापसी | अतिरिक्त | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | --- |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | --- | --- | 10000000 |
एक ही सिद्धांत का उपयोग दशमलव संख्याओं के कंप्यूटर प्रतिनिधित्व में किया जा सकता है: प्रत्येक अंक के लिए, अंक X को 9 - X से बदल दिया जाता है, और परिणामी संख्या को जोड़ा जाता है। उदाहरण के लिए, चार-अंकीय संख्या used0081 का उपयोग करते समय, इसे 9919 (9919 + 0081 = 0000, पांचवें अंक) से बदल दिया जाता है। फेंका हुआ)।
समान विचार को सामान्य 10-बिट नंबर सिस्टम पर लागू करते समय, यह बाहर निकलेगा (उदाहरण के लिए, 10-बिट नंबर सिस्टम का उपयोग करके काल्पनिक प्रोसेसर के लिए):
| 10 वीं अंक प्रणाली ("सामान्य" प्रविष्टि) |
10 वीं अंक प्रणाली अतिरिक्त कोड |
|---|---|
| ... | ... |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| ... | ... |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| ... | ... |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| ... | ... |
एक संख्या को एक प्रत्यक्ष कोड से एक अतिरिक्त में बदलना निम्नलिखित एल्गोरिथम के अनुसार किया जाता है।
एक उदाहरण है। हम डायरेक्ट कोड में लिखी गई ऋणात्मक संख्या written5 को एक अतिरिक्त में बदल देते हैं। नंबर taken5 लिया मॉडुलो का सीधा कोड:
रिवर्स कोड:
परिणाम 1 में जोड़ें
हमें बाईं ओर एक अंक जोड़ें।
व्युत्क्रम परिवर्तन के लिए, एक ही एल्गोरिदम का उपयोग किया जाता है। अर्थात्:
हम संख्या के सभी अंकों को पलटाते हैं, इस प्रकार एक रिवर्स कोड प्राप्त करते हैं:
परिणाम 1 में जोड़ें
और अतिरिक्त कोड के साथ जोड़कर जांच करें
0101 + 1011 = 10000, पांचवा अंक फेंका गया है।
सिस्टम में पी-आधार नंबर संख्या को उसके अतिरिक्त कोड में परिवर्तित करके संख्या के चिह्न को बदलते हैं। उदाहरण के लिए, यदि 5-संख्या अंक प्रणाली का उपयोग किया जाता है, तो 1000 के विपरीत संख्या ... (1) 4444 है .... (.1)।
यदि ए< 0 then a := ((not a ) or 128 ) + 1 ;
इंट कन्वर्ट (int) (यदि (ए)< 0 ) a = ( ~- a | 128 ) + 1 ; return a ; }